��Ŀ����
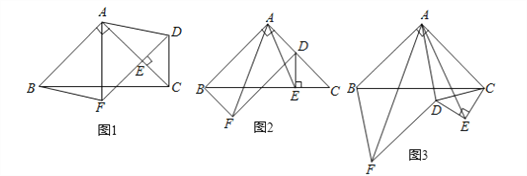
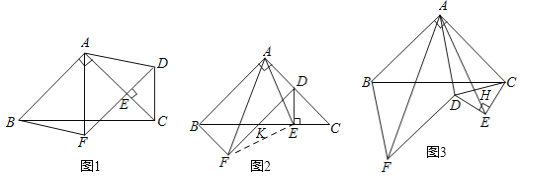
����Ŀ����ͼ1���ڵ���Rt��ABC������BAC=90������E��AC�ϣ��Ҳ����A��C�غ���������ABC���ⲿ������Rt��CED��ʹ��CED=90��������AD���ֱ���AB��ADΪ�ڱ���ƽ���ı���ABFD������AF��
��1����֤����AEF�ǵ���ֱ����������
��2����ͼ2������CED�Ƶ�C��ʱ����ת������E���߶�BC��ʱ������AE����֤��AF=![]() AE��
AE��
��3����ͼ3������CED�Ƶ�C������ʱ����ת����ƽ���ı���ABFDΪ����������CED����ABC���·�ʱ����AB=2![]() ��CE=2�����߶�AE�ij���
��CE=2�����߶�AE�ij���
���𰸡���1���𰸼���������2���𰸼���������3��4![]() ��
��
�������������������1������AE=EF����DEC=��AEF=90�㣬����֤����AEF�ǵ���ֱ����������
��2������EF��DF��BC��K����֤����EKF�ա�EDA����֤����AEF�ǵ���ֱ�������μ��ɵó�������
��3����AD=AC=ABʱ���ı���ABFD�������������EH=DH=CH=![]() ��Rt��ACH����AH=3
��Rt��ACH����AH=3![]() �����ɵõ�AE=AH+EH=4
�����ɵõ�AE=AH+EH=4![]() ��
��
���������������1����ͼ1�����ı���ABFD��ƽ���ı�������AB=DF����AB=AC����AC=DF����DE=EC����AE=EF���ߡ�DEC=��AEF=90�㣬���AEF�ǵ���ֱ����������
��2����ͼ2������EF��DF��BC��K�����ı���ABFD��ƽ���ı�������AB��DF�����DKE=��ABC=45�㣬���EKF=180�㩁��DKE=135�㣬EK=ED���ߡ�ADE=180�㩁��EDC=180�㩁45��=135�㣬���EKF=��ADE���ߡ�DKC=��C����DK=DC����DF=AB=AC����KF=AD������EKF�͡�EDA���� 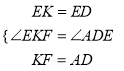 �����EKF�ա�EDA��SAS������EF=EA����KEF=��AED�����FEA=��BED=90�㣬���AEF�ǵ���ֱ������������AF=
�����EKF�ա�EDA��SAS������EF=EA����KEF=��AED�����FEA=��BED=90�㣬���AEF�ǵ���ֱ������������AF=![]() AE��
AE��
��3����ͼ3����AD=AC=ABʱ���ı���ABFD����������AE��CD��H������AD=AC��ED=EC���ɵ�AE��ֱƽ��CD����CE=2����EH=DH=CH=![]() ��Rt��ACH����AH=
��Rt��ACH����AH=![]() =3
=3![]() ����AE=AH+EH=4
����AE=AH+EH=4![]() ��
��

����Ŀ��ij�ֳ�Ҫ����һ��������һ�������µ���ֲ�ɻ��ʣ�����ֲ�����е�ͳ�ƽ�����±���ʾ��
��ֲ������n/�� | 500 | 1000 | 2000 | 4000 | 7000 | 10000 | 12000 | 15000 |
�ɻ������m/�� | 423 | 868 | 1714 | 3456 | 6020 | 8580 | 10308 | 12915 |
�ɻ��Ƶ�� | 0.846 | 0.868 | 0.857 | 0.864 | 0.860 | 0.858 | 0.859 | 0.861 |
�ڴ������£����Ƹ���������ֲ�ɻ�ĸ���Ϊ_________________����ȷ��![]() ���������ֳ���ʹ�ɻ�������ﵽ4.3��ã��������Ҫ��ֲ��������_________���.
���������ֳ���ʹ�ɻ�������ﵽ4.3��ã��������Ҫ��ֲ��������_________���.
����Ŀ��ijũ�����ס������������ˮ��3�����Ϊ�˿���ˮ���볤���������ͬһ������������������ֱ������ȡ��![]() ��������в�������������ǵij���
��������в�������������ǵij���![]() ����λ��cm�����������ݣ��볤�������������������ͷ���.��������˲�����Ϣ.
����λ��cm�����������ݣ��볤�������������������ͷ���.��������˲�����Ϣ.
a.���������볤��Ƶ���ֲ�ͳ�Ʊ����±���ʾ������������
���������볤Ƶ���ֲ���
����/ | Ƶ�� | Ƶ�� |
| 4 | 0.08 |
| 9 | 0.18 |
|
| |
| 11 | 0.22 |
|
| 0.20 |
| 2 | |
�ϼ� | 50 | 1.00 |
b.���������볤��Ƶ���ֲ�ֱ��ͼ��ͼ��ʾ��
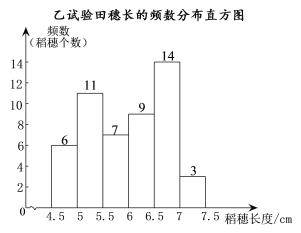
c.���������볤��![]() ��һ����ǣ�
��һ����ǣ�
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.�ס����������볤��ƽ��������λ�����������������£���2����
������ | ƽ���� | ��λ�� | ���� | ���� |
�� | 5.924 | 5.8 | 5.8 | 0.454 |
�� | 5.924 |
| 6.5 | 0.608 |
����������Ϣ���ش��������⣺
��1������![]() ��ֵΪ ��
��ֵΪ ��![]() ��ֵΪ ��
��ֵΪ ��
��2������![]() ��ֵΪ ��
��ֵΪ ��
��3���ڴ˴ο����У��������������ȣ����ȶ����������� ��
A���� B���� C�����ƶ�
��4�����볤��![]() ��Χ�ڵĵ���Ϊ�����á�������Ƽ����������С����á���ˮ��ԼΪ �����
��Χ�ڵĵ���Ϊ�����á�������Ƽ����������С����á���ˮ��ԼΪ �����