题目内容
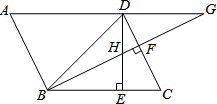 如图,已知?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:
如图,已知?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=
| 2 |
其中正确的结论是( )
| A、①②③④ | B、①②③ |
| C、①②④ | D、②③④ |
分析:根据已知及相似三角形的判定方法对各个结论进行分析从而得到最后答案.
解答:解:∵∠BDE=45°,DE⊥BC
∴DB=
BE,BE=DE
∵DE⊥BC,BF⊥CD
∴∠BEH=∠DEC=90°
∵∠BHE=∠DHF
∴∠EBH=∠CDE
∴△BEH≌△DEC
∴∠BHE=∠C,BH=CD
∵?ABCD中
∴∠C=∠A,AB=CD
∴∠A=∠BHE,AB=BH
∴正确的有①②③
故选B.
∴DB=
| 2 |
∵DE⊥BC,BF⊥CD
∴∠BEH=∠DEC=90°
∵∠BHE=∠DHF
∴∠EBH=∠CDE
∴△BEH≌△DEC
∴∠BHE=∠C,BH=CD
∵?ABCD中
∴∠C=∠A,AB=CD
∴∠A=∠BHE,AB=BH
∴正确的有①②③
故选B.
点评:此题考查了相似三角形的判定和性质:①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.相似三角形的对应边成比例,对应角相等.

练习册系列答案
相关题目
 14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是
14、如图,已知?ABCD中,AB=4,BC=6,BC边上的高AE=2,则DC边上的高AF的长是

 26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
26、如图,已知?ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.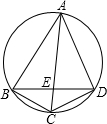 如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于
如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于 如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.