Question

【题目】如图，AB、CD是两个过江电缆的铁塔，塔AB高40米，AB的中点为P，塔底B距江面的垂直高度为6米．跨江电缆因重力自然下垂近似成抛物线形，为了保证过往船只的安全，电缆下垂的最低点距江面的高度不得少于30米．已知：人在距塔底B点西50米的地面E点恰好看到点E、P、C在一直线上；再向西前进150米后从地面F点恰好看到点F、A、C在一直线上．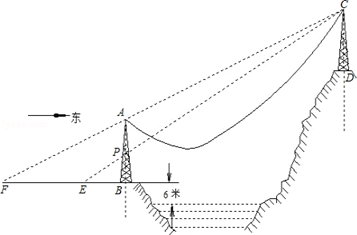

（1）求两铁塔轴线间的距离（即直线AB、CD间的距离）；
（2）若以点A为坐标原点，向东的水平方向为x轴，取单位长度为1米，BA的延长方向为y轴建立坐标系．求刚好满足最低高度要求的这个抛物线的解析式．

Answer 1

【答案】
（1）

解：如图，AB=40米，BP=20米，BE=50米，BF=50+150=200（米）．

设CD的延长线交地平面于点H．

设CH=x，BH=y

由△EBP∽△EHC得 = ，即 = ①

由△FBA∽△FHC得 = ，即 = ②

由①②解得：x=60，y=100

答：两铁塔轴线间的距离为100米；

（2）

解：依题意建立坐标系如图，由（1）得CH=60米，C点比A点高20米，

这时A、C两点的坐标为：A（0，0），C（100，20），

设抛物线顶点为P（x0，y0），

因为要求最低点高于地面为30﹣6=24（米），点A高度为40米，所以y0=﹣16．

设过点A的抛物线解析式为y=ax2+bx（a＞0），则该抛物线满足：

化简得：125b2+80b﹣16=0

解得：b1= ，b2=﹣

∵抛物线的对称轴在y轴的右侧，有 ＞0，而a＞0

∴b＜0，故b1= 舍去

把b2=﹣ 代入前式得：a=

∴y= x2﹣ x

答：所求抛物线的解析式为y= x2﹣ x．

【解析】（1）根据题意，连接CA并延长到F，连接CP并延长到E，CD的延长线交地平面于点H．于是构造了两对相似三角形：EBP∽△EHC，△FBA∽△FHC，利用相似三角形的性质，建立起AB、CD之间的关系式，解方程组即可；（2）因为点A为坐标原点，则可设过原点的二次函数解析式为y=ax2+bx（a＞0），将C（100，20）代入上式可得关于a、b的关系式，再根据二次函数顶点坐标公式和最低点高于地面为30﹣6=24（米），点A高度为40米，得到关于a、b的关系式，于是可以求出二次函数解析式．
【考点精析】通过灵活运用关于坡度坡角问题，掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA即可以解答此题．