��Ŀ����
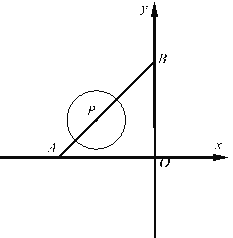
����Ŀ����ͼ��1������ƽ��ֱ������ϵ�У�����ABCO��B������Ϊ��4��3����������y= ![]() x2+bx+c��������ABCO�Ķ���B��C��DΪBC���е㣬ֱ��AD��y�ύ��E�㣬��������y=
x2+bx+c��������ABCO�Ķ���B��C��DΪBC���е㣬ֱ��AD��y�ύ��E�㣬��������y= ![]() x2+bx+c���ڵ�������F�㣮
x2+bx+c���ڵ�������F�㣮
��1����������߽���ʽ��F�����ꣻ
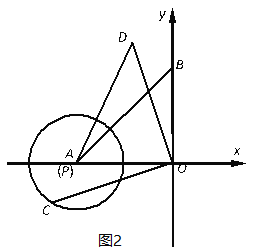
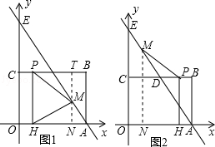
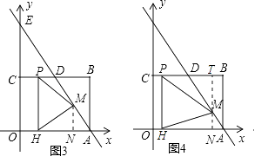
��2����ͼ��2��������P�ӵ�C���������߶�CB��ÿ��1����λ���ȵ��ٶ����յ�B�˶���ͬʱ������M�ӵ�A���������߶�AE��ÿ�� ![]() ����λ���ȵ��ٶ����յ�E�˶�������P��PH��OA������ΪH������MP��MH�����P���˶�ʱ��Ϊt��
����λ���ȵ��ٶ����յ�E�˶�������P��PH��OA������ΪH������MP��MH�����P���˶�ʱ��Ϊt��
����EP+PH+HF�Ƿ�����Сֵ������У����t��ֵ�����û�У���˵�����ɣ�
������PMH�ǵ��������Σ���ֱ��д����ʱt��ֵ��
���𰸡�
��1��
�⣺�߾���ABCO��B������Ϊ��4��3��
��C��������0��3��
��������y= ![]() x2+bx+c��������ABCO�Ķ���B��C��
x2+bx+c��������ABCO�Ķ���B��C��
�� ![]() ��
��
��ã� ![]() ��
��
��������߽���ʽy=�� ![]() x2+2x+3��
x2+2x+3��
��ֱ��AD�Ľ���ʽΪy=k1x+b1
��A��4��0����D��2��3����
�� ![]() ��
��  ��
��
�� ![]() ��
��
���� 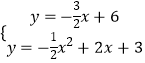 ��
��
��F���ڵ������ޣ�
��F��6����3����
��2��
�⣺�١�E��0��6������CE=CO������ͼ��1������

����CF��x����H�䣬��H����BC�Ĵ��߽�BC��P�䣬��P
�˶���P�䣬��H�˶���H��ʱ��EP+PH+HF��ֵ��С��
��ֱ��CF�Ľ���ʽΪy=k2x+b2
��C��0��3����F��6����3����
�� ![]() ��
��
��ã� ![]() ��
��
��y=��x+3
��y=0ʱ��x=3��
��H�䣨3��0����
��CP=3����t=3��
����ͼ1��M��MN��OA��OA��N��
�ߡ�AMN�ס�AEO��
�� ![]() ��
��
�� ![]() ��
��
��AN=t��MN= ![]() ��
��
I��ͼ3����PM=HMʱ��M��PH�Ĵ�ֱƽ�����ϣ�
��MN= ![]() PH��
PH��
��MN= ![]() ��
��
��t=1��
II��ͼ1����HM=HPʱ��MH=3��MN= ![]() ��
��
HN=OA��AN��OH=4��2t ��Rt��HMN��MN2+HN2=MH2��
�� ![]() ��
��
��25t2��64t+28=0��
��ã�t1=2����ȥ���� ![]() ��
��
III��ͼ2��ͼ4����PH=PMʱ��
��PM=3��MT= ![]() ��PT=BC��CP��BT=|4��2t|��
��PT=BC��CP��BT=|4��2t|��
����Rt��PMT��MT2+PT2=PM2��
�� ![]() ��
��
��25t2��100t+64=0��
��ã� ![]() ��
�� ![]()
���������� ![]() ��
�� ![]() ��1��
��1�� ![]() ��
��
����������1���ɾ��ε����ʿ����C������꣬��B��C����������y= ![]() x2+bx+c���b��c��ֵ���ɸ������߽���ʽ����ֱ��AD�Ľ���ʽΪy=k1x+b1��A��4��0����D��2��3���������һ�κ����Ľ���ʽ�����������κ�����һ�κ����Ľ���ʽ�������F������ꣻ��2��������CF��x����H�䣬��H����BC�Ĵ��߽�BC��P�䣬��P�˶���P�䣬��H�˶���H��ʱ��EP+PH+HF��ֵ��С���ڹ�M��MN��OA��OA��N���ٷֱ����۵�PM=HMʱ��M��PH�Ĵ�ֱƽ�����ϣ���PH=PMʱ��������������tֵ���ɣ�
x2+bx+c���b��c��ֵ���ɸ������߽���ʽ����ֱ��AD�Ľ���ʽΪy=k1x+b1��A��4��0����D��2��3���������һ�κ����Ľ���ʽ�����������κ�����һ�κ����Ľ���ʽ�������F������ꣻ��2��������CF��x����H�䣬��H����BC�Ĵ��߽�BC��P�䣬��P�˶���P�䣬��H�˶���H��ʱ��EP+PH+HF��ֵ��С���ڹ�M��MN��OA��OA��N���ٷֱ����۵�PM=HMʱ��M��PH�Ĵ�ֱƽ�����ϣ���PH=PMʱ��������������tֵ���ɣ�
�����㾫����ͨ������������������ε����ʣ����ն�Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������μ����Խ����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�