Ő‚ńŅńŕ»›
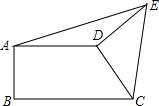
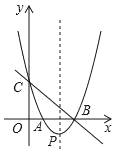
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨÷ĪŌŖy£Ĺ©Āx+3”Žx÷Š°Ęy÷Š∑÷ĪūĹĽ”ŕB°ĘCŃĹĶ„£¨ĺ≠ĻżB°ĘCŃĹĶ„ĶńŇ◊őÔŌŖy£Ĺx2+bx+c”Žx÷ŠĶńŃŪ“ĽłŲĹĽĶ„ő™A£¨∂•Ķ„ő™P£ģ
£®1£©«ůł√Ň◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
£®2£©ĶĪ0£ľx£ľ3 Ī£¨‘ŕŇ◊őÔŌŖ…Ō«ů“ĽĶ„E£¨ Ļ°ųCBEĶń√śĽż”–◊Óīů÷Ķ£Ľ
£®3£©‘ŕł√Ň◊őÔŌŖĶń∂‘≥∆÷Š…Ō «∑Ůīś‘ŕĶ„M£¨ Ļ“‘C°ĘP°ĘMő™∂•Ķ„Ķń»żĹ«–őő™Ķ»—Ł»żĹ«–ő£Ņ»Űīś‘ŕ£¨«Ž–ī≥Ųňý∑ŻļŌŐűľĢĶńĶ„MĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©y£Ĺx2©Ā4x+3£Ľ£®2£©E£®![]() £¨©Ā
£¨©Ā![]() £©£Ľ£®3£©£®2£¨7£©ĽÚ£®2£¨©Ā1+2
£©£Ľ£®3£©£®2£¨7£©ĽÚ£®2£¨©Ā1+2![]() £Ĺ£©ĽÚ£®2£¨©Ā1©Ā2
£Ĺ£©ĽÚ£®2£¨©Ā1©Ā2![]() £©ĽÚ£®2£¨
£©ĽÚ£®2£¨![]() £©
£©
°ĺĹ‚őŲ°Ņ
£®1£©”√÷ĪŌŖĪŪīÔ Ĺ«ů≥ŲĶ„B°ĘCĶń◊ÝĪÍ£¨ĹęĶ„B°ĘCĶń◊ÝĪÍīķ»Žy£Ĺx2+bx+c£¨ľīŅ…«ůĹ‚£Ľ
£®2£©S°ųCBE£Ĺ![]() HE°ŃOB£Ĺ
HE°ŃOB£Ĺ![]() °Ń3°Ń£®©Āx+3©Āx2+4x©Ā3£©£Ĺ
°Ń3°Ń£®©Āx+3©Āx2+4x©Ā3£©£Ĺ![]() £®©Āx2+3x£©£¨ľīŅ…«ůĹ‚£Ľ
£®©Āx2+3x£©£¨ľīŅ…«ůĹ‚£Ľ
£®3£©∑÷CM£ĹCP°ĘCP£ĹPM°ĘCM£ĹPM»ż÷÷«ťŅŲ£¨∑÷Īū«ůĹ‚ľīŅ…£ģ
Ĺ‚£ļ£®1£©y£Ĺ©Āx+3£¨ŃÓy£Ĺ0£¨‘Úx£Ĺ3£¨ŃÓx£Ĺ0£¨‘Úy£Ĺ3£¨
Ļ Ķ„B°ĘCĶń◊ÝĪÍő™£®3£¨0£©°Ę£®0£¨3£©£¨
ĹęĶ„B°ĘCĶń◊ÝĪÍīķ»Žy£Ĺx2+bx+c≤ĘĹ‚Ķ√£ļb£Ĺ©Ā4£¨
Ļ Ň◊őÔŌŖĶńĪŪīÔ Ĺő™£ļy£Ĺx2©Ā4x+3£¨
ŃÓy£Ĺ0£¨‘Úx£Ĺ1ĽÚ3£¨Ļ Ķ„A£®1£¨0£©£¨Ķ„P£®2£¨©Ā1£©£Ľ
£®2£©ĻżĶ„E◊ųEH°őy÷ŠĹĽBC”ŕĶ„H£¨
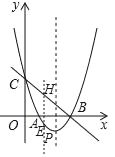
…ŤĶ„E£®x£¨x2©Ā4x+3£©£¨‘ÚĶ„H£®x£¨©Āx+3£©
S°ųCBE£Ĺ![]() HE°ŃOB£Ĺ
HE°ŃOB£Ĺ![]() °Ń3°Ń£®©Āx+3©Āx2+4x©Ā3£©£Ĺ
°Ń3°Ń£®©Āx+3©Āx2+4x©Ā3£©£Ĺ![]() £®©Āx2+3x£©£¨
£®©Āx2+3x£©£¨
°Ŗ©Ā![]() £ľ0£¨ĶĪx£Ĺ
£ľ0£¨ĶĪx£Ĺ![]() Ī£¨S°ųCBE”–◊Óīů÷Ķ£¨
Ī£¨S°ųCBE”–◊Óīů÷Ķ£¨
Ķ„E£®![]() £¨©Ā
£¨©Ā![]() £©£Ľ
£©£Ľ
£®3£©Ķ„C£®0£¨3£©°ĘĶ„P£®2£¨©Ā1£©£¨…ŤĶ„M£®2£¨m£©£¨
CP2£Ĺ4+16£Ĺ20£¨CM2£Ĺ4+£®m©Ā3£©2£Ĺm2©Ā6m+13£¨PM2£Ĺm2+2m+1£¨
ĘŔĶĪCM£ĹCP Ī£¨20£Ĺm2©Ā6m+13£¨Ĺ‚Ķ√£ļm£Ĺ7ĽÚ©Ā1£®…Š»•m£Ĺ©Ā1£©£Ľ
ĘŕĶĪCP£ĹPM Ī£¨Õ¨ņŪŅ…Ķ√£ļm£Ĺ©Ā1°ņ2![]() £Ľ
£Ľ
ĘŘĶĪCM£ĹPM Ī£¨Õ¨ņŪŅ…Ķ√£ļm£Ĺ![]() £Ľ
£Ľ
Ļ Ķ„M◊ÝĪÍő™£ļ£®2£¨7£©ĽÚ£®2£¨©Ā1+2![]() £Ĺ£©ĽÚ£®2£¨©Ā1©Ā2
£Ĺ£©ĽÚ£®2£¨©Ā1©Ā2![]() £©ĽÚ£®2£¨
£©ĽÚ£®2£¨![]() £©£ģ
£©£ģ