题目内容
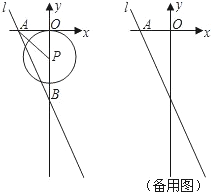
如图,在平面直角坐标系中,直线 =
=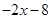 分别与
分别与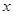 轴,
轴, 轴相交于
轴相交于 两点,点
两点,点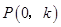 是
是 轴的负半轴上的一个动点,以
轴的负半轴上的一个动点,以 为圆心,3为半径作
为圆心,3为半径作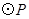 .
.
(1)连结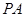 ,若
,若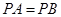 ,试判断
,试判断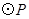 与
与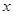 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(2)当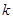 为何值时,以
为何值时,以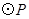 与直线
与直线 =
=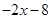 的两个交点和圆心
的两个交点和圆心 为顶点的三角形是正三角形?
为顶点的三角形是正三角形?
 =
=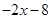 分别与
分别与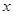 轴,
轴, 轴相交于
轴相交于 两点,点
两点,点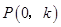 是
是 轴的负半轴上的一个动点,以
轴的负半轴上的一个动点,以 为圆心,3为半径作
为圆心,3为半径作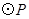 .
.(1)连结
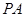 ,若
,若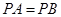 ,试判断
,试判断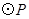 与
与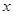 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;(2)当
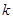 为何值时,以
为何值时,以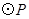 与直线
与直线 =
=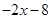 的两个交点和圆心
的两个交点和圆心 为顶点的三角形是正三角形?
为顶点的三角形是正三角形?
(1)⊙P与x轴相切.理由见解析;(2)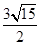 -8或k=-
-8或k=-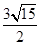 -8
-8
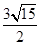 -8或k=-
-8或k=-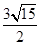 -8
-8试题分析:(1)通过一次函数可求出A、B两点的坐标及线段的长,再在Rt△AOP利用勾股定理可求得当PB=PA时k的值,再与圆的半径相比较,即可得出⊙P与x轴的位置关系.
(2)根据正三角形的性质,分两种情况讨论,
①当圆心P在线段OB上时,②当圆心P在线段OB的延长线上时,从而求得k的值.
试题解析:(1)⊙P与x轴相切,
∵直线y=-2x-8与x轴交于A(-4,0),与y轴交于B(0,-8),
∴OA=4,OB=8.
由题意,OP=-k,
∴PB=PA=8+k.
∵在Rt△AOP中,k2+42=(8+k)2
∴k=-3,
∴OP等于⊙P的半径.
∴⊙P与x轴相切.
(2)设⊙P1与直线l交于C,D两点,连接P1C,P1D,
当圆心P1在线段OB上时,作P1E⊥CD于E,
∵△P1CD为正三角形,
∴DE=
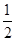 CD=
CD=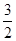 ,P1D=3.
,P1D=3.∴P1E=
 .
.∵∠AOB=∠P1EB=90°,∠ABO=∠P1BE,
∴△AOB∽△P1EB.
∴
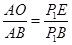 ,即
,即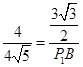 ,
,∴P1B=
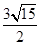 .
.∴P1O=BO-BP1=8-
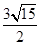 .
.∴P1(0,
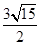 -8).
-8).∴k=
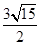 -8.
-8.当圆心P2在线段OB延长线上时,同理可得P2(0,-
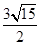 -8).
-8).∴k=-
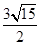 -8.
-8.∴当k=
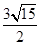 -8或k=-
-8或k=-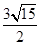 -8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.
-8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.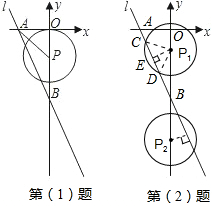

练习册系列答案
相关题目

 ,则OD= .
,则OD= .


 = .
= .