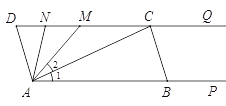
جâؤ؟ؤعبف
،¾جâؤ؟،؟شعز»¸ِ؟ع´üضذسذ4¸ِحêب«دàح¬µؤذ،اٍ£¬°رثüأا·ض±ً±ê؛إ1،¢2،¢3،¢4£®ذ،أ÷دبثو»ْµطأ³ِز»¸ِذ،اٍ£¬ذ،ا؟شظثو»ْµطأ³ِز»¸ِذ،اٍ£®¼اذ،أ÷أ³ِاٍµؤ±ê؛إخھx£¬ذ،ا؟أ³ِµؤاٍ±ê؛إخھy£®ذ،أ÷؛حذ،ا؟شع´ث»ù´،ةد¹²ح¬ذةجز»¸ِسخد·¹وشٍ£؛µ±x£¾yت±ذ،أ÷»ٌت¤،£·ٌشٍذ،ا؟»ٌت¤£®
(1)بôذ،أ÷أ³ِµؤاٍ²»·إ»ط£¬اَذ،أ÷»ٌت¤µؤ¸إآت£»
(2)بôذ،أ÷أ³ِµؤاٍ·إ»ط؛َذ،ا؟شظثو»ْأاٍ£¬ختثûأاضئ¶¨µؤسخد·¹وشٍ¹«ئ½آً?اëثµأ÷ہيسة£®
،¾´ً°¸،؟£¨1£©![]() £¨2£©²»¹«ئ½£¬ہيسة¼û½âخِ£®
£¨2£©²»¹«ئ½£¬ہيسة¼û½âخِ£®
،¾½âخِ،؟تشجâ·ضخِ£؛£¨1£©»ت÷×´ح¼µأ³ِثùسذµب؟ةؤـµؤ½ل¹û¹²12ضض£¬¶ّذ،أ÷»ٌت¤µؤسذ6ضضاé؟ِ£¬ب»؛َہûسأ¸إآت¹«ت½¼ئثم¼´؟ة£»£¨2£©ح¨¹»ت÷×´ح¼£¬·ض±ًاَ³ِذ،أ÷»ٌت¤؛حذ،ا؟»ٌت¤µؤ¸إآت£¬±ب½د´َذ،¼´؟ة£¬¸إآتدàµب£¬سخد·¹«ئ½£¬·ٌشٍ²»¹«ئ½£®
تشجâ½âخِ£؛½â£؛£¨1£©»ت÷×´ح¼µأ£؛
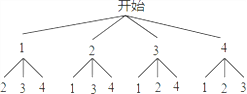
،ك¹²سذ12ضضµب؟ةؤـµؤ½ل¹û£¬
ذ،أ÷»ٌت¤µؤسذ£¨2£¬1£©£¬£¨3£¬1£©£¬£¨3£¬2£©£¬£¨4£¬1£©£¬£¨4£¬2£©£¬£¨4£¬3£©¹²6ضضاé؟ِ£¬
،àذ،أ÷»ٌت¤µؤ¸إآتخھ£؛![]() =
=![]() £»
£»
£¨2£©»ت÷×´ح¼µأ£؛
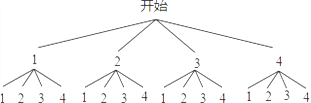
،ك¹²سذ16ضضµب؟ةؤـµؤ½ل¹û£¬
ذ،أ÷»ٌت¤µؤسذ£¨2£¬1£©£¬£¨3£¬1£©£¬£¨3£¬2£©£¬£¨4£¬1£©£¬£¨4£¬2£©£¬£¨4£¬3£©¹²6ضضاé؟ِ£¬
،àP£¨ذ،أ÷»ٌت¤£©=![]() =
=![]() £¬P£¨ذ،ا؟»ٌت¤£©=
£¬P£¨ذ،ا؟»ٌت¤£©=![]() £¬
£¬
،كP£¨ذ،أ÷»ٌت¤£©،ظP£¨ذ،ا؟»ٌت¤£©£¬
،àثûأاضئ¶¨µؤسخد·¹وشٍ²»¹«ئ½£®

،¾جâؤ؟،؟شع¹ْ¼ز³«µ¼دآ£¬،°ب«أٌشؤ¶ء،±صضً²½×كدٍئص¼°£¬ر§ذ£زھاَح¬ر§أاشع¼زہïہûسأدذد¾ت±¹â¶à¶ءذ©سذزوµؤتé¼®. حُ¸صح¬ر§شع±¾ر§ئع؟ھر§³ُ¶ش±¾ؤ꼶²؟·ضح¬ر§؛®¼ظشع¼زئ½¾ùأ؟جى¶ءتéµؤز³ت½ّذذءث³éرùµ÷²é£¨½ل¹ûب،صûت£©£¬ثùµأت¾فح³¼ئبçدآ±ي£؛
¶ءتéز³ت | 0.5~20.5 | 20.5~40.5 | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 |
ئµ ت | 20 | 25 | 30 | 15 | 10 |
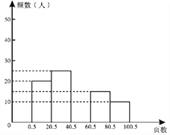
£¨1£©³éب،رù±¾µؤبفء؟تا .
£¨2£©¸ù¾ف±يضذت¾ف²¹ب«ح¼ضذµؤئµت·ض²¼ض±·½ح¼.
£¨3£©رù±¾µؤضذخ»تثùشعµؤ·¶خ§تا .
£¨4£©بô¸أؤ꼶سذر§ةْ1060بث£¬ؤاأ´´َش¼سذ¶àةظر§ةْشع؛®¼ظئ½¾ùأ؟جى¶ءتé60.5~100.5ز³ض®¼ن£؟