题目内容
【题目】(8分) 如图,点C、M、N在射线DQ上,点B在射线AP上,且AP∥DQ,∠D=∠ABC=80°,∠1=∠2,AN平分∠DAM.
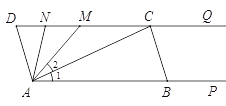
(1)试说明AD∥BC的理由;
(2)试求∠CAN的度数;
(3)平移线段BC.
①试问∠AMD:∠ACD的值是否发生变化?若不会,请求出这个比值;若会,请找出相应变化规律;
②若在平移过程中存在某种位置,使得∠AND=∠ACB,试求此时∠ACB的度数.
【答案】(1)见解析;(2) ∠CAN=50°;(3)①不会, ∠AMD:∠ACD=2;②∠ACB=75°.
【解析】试题分析:(1)由平行线的性质和判定即可得到结论;
(2)由角平分线的定义和角的和差可以得到结论;
(3)①不会.根据平行线的性质即可得到结论;
②由平行线的性质和∠AND=∠ACB,得到∠NAB=∠DAC,进而得到∠1=∠DAN,即可得到结论.
试题解析:解:(1)∵AP∥DQ,∴∠D+∠DAB=180°.
∵∠D=80°,∴∠DAB=100°.
∵∠ABC=80°,∴∠DAB+∠ABC=180°,∴AD∥BC.
(2)∵AN平分∠DAM,∴∠NAM=∠NAD=![]() ∠DAM.
∠DAM.
∵∠1=∠2, ∴∠CAM=![]() ∠BAM.
∠BAM.
∴∠NAM+∠CAM=![]() ∠DAM+
∠DAM+![]() ∠BAM,
∠BAM,
即:∠CAN=![]() ∠DAB
∠DAB
∵∠DAB=100°,∴∠CAN=50°.
(3)①不会.
∵AP∥DQ,∴∠AMD=∠MAB=2∠1,∠ACD=∠1,
∴∠AMD:∠ACD=2.
②∵AP∥DQ,AD∥BC,∴∠AND=∠NAB,∠ACB=∠DAC.
∵∠AND=∠ACB,∴∠NAB=∠DAC,∴∠NAB-∠NAC=∠DAC-∠NAC,即:∠1=∠DAN,∴∠1=∠2=∠DAN=∠MAN=25°,∴∠ACB=∠DAC=75°.

 阅读快车系列答案
阅读快车系列答案【题目】某学习小组,在探究1+![]() 的性质时,得到了如下数据:
的性质时,得到了如下数据:
x | 1 | 10 | 100 | 1000 | 10000 | … |
1+ | 3 | 1.2 | 1.02 | 1.002 | 1.0002 | … |
根据表格中的数据,做出了四个推测:
①1+![]() (x>0)的值随着x的增大而减小;
(x>0)的值随着x的增大而减小;
②1+![]() (x>0)的值有可能等于1;
(x>0)的值有可能等于1;
③1+![]() (x>0)的值随着x的增大越来越接近于1;
(x>0)的值随着x的增大越来越接近于1;
④1+![]() (x>0)的值最大值是3.则推测正确的有( )
(x>0)的值最大值是3.则推测正确的有( )
A.1个
B.2个
C.3个
D.4个