题目内容
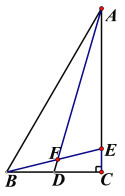
【题目】如图，在某校图书馆门前一段笔直的内部道路AB上，过往车辆限速3米/秒在点B的正上方距其7米高的C处有一个探测仪．一辆轿车从点A匀速向点B行驶5秒后此轿车到达D点，探测仪测得∠CAB＝18°，∠CDB＝45°，求AD之间的距离，并判断此轿车是否超速，（结果精确到0.01米）（参考数据：sinl8°＝0.309，cosl8°＝0.951，tanl8°＝0.325）
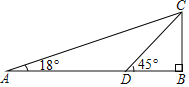
【答案】此轿车没有超速
【解析】
根据直角三角形的性质和三角函数解答即可．
由题意可得：在Rt△BCD中，∠CBD＝90°，∠CDB＝45°，
∴∠DCB＝∠CDB＝45°，
∴BC＝BD＝7，
在Rt△ABC中，∠BAC＝18°，BC＝7，
tan∠BAC＝
，
∴AB=
=
21.538，
∴AD＝21.538﹣7＝14.538≈14.54，
14.54÷5≈2.91＜3，
答：AD之间的距离约为14.54米，此轿车没有超速．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
