题目内容
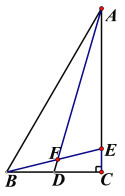
【题目】Rt△ABC中，∠C＝90°， ∠BAC＝30°, BC＝84. D,E分别在射线BC,AC上, AD与BE交于F.
(1)从顶点A所作三角形中线长为_______;
(2)若D恰为BC边中点, E在边AC上且AE:EC＝6:1, 求∠AFE.
(3) 当AD与BE所成锐角为60°,求CE.
【答案】（1）42
（2）60°（3）
.
【解析】
（1）先根据已知条件解得AC的长，因为从顶点A所作三角形中线，所以是连接点A和对边BC中点的线段，根据勾股定理可得结果；(2) 在Rt△BCE中，tan∠CBE=
= 
=
, 过点D作DN⊥AB于点N，因为S△ABD=
×BD×AC=×AB×DN，即BD×AC= AB×DN，42×84
=168×DN，解得：DN=21，可得tan∠NAD＝
= 
=，所以∠CBE=∠BAD，从而∠AFE=∠BAD+ABF=∠BAD+ ∠CBE= 60°.(3) 因为条件是AD与BE所成锐角为60°，（2）中正好满足此条件，所以在（2）的条件下，通过证明△ABF∽△ADB，求出AD=
，再过点F作FG//BC交AC于与G,得比例式DC:FG=AD:AF，从而求解.
解：.(1)∵∠C＝90°， ∠BAC＝30°, BC＝84，
∴AB=2BC=168，AC=BC=84,当D恰好是BC的中点时，CD=BC=42，
在Rt△ACD中，AD=
=
= 42.
(2) ∵D恰为BC边中点, E在边AC上且AE:EC＝6:1,∴BD=DC=42，CE=
AC=12,
在Rt△BCE中，tan∠CBE== =.
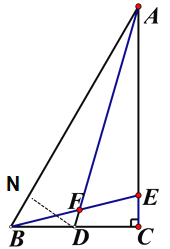
过点D作DN⊥AB于点N， ∵S△ABD=×BD×AC=×AB×DN，即BD×AC= AB×DN，42×84=168×DN，解得：DN=21，
在Rt△AND中，∵AN=
=147，∴tan∠NAD＝= =.
∴∠CBE=∠BAD，从而∠AFE=∠BAD+ABF=∠BAD+ ∠CBE= 60°.
(3)∵（2）中AD与BE所成锐角为60°，所以在（2）的条件下：
∵∠CBE=∠BAD，∠BDF=∠ADB ∴△ABF∽△ADB,
∴AB=AF·AD，解得：AD=.
过点F作FG//BC交AC于与G,
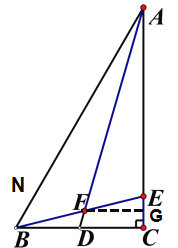
DC:FG=AD:AF=13:16,
CG=84×3√3/13
FG:BC=16:26,
EC:CG=26:10
EC=252√3/5.
