题目内容
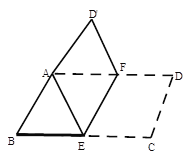
【题目】在菱形![]() 中,点
中,点![]() 是对角线的交点,点
是对角线的交点,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 在
在![]() 延长线上,且
延长线上,且![]() .
.
![]() 求证:
求证:![]() ;
;
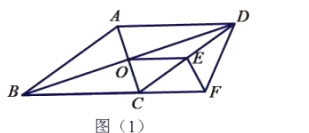
![]() 如果
如果![]() ,请写出图中所有的等边三角形.
,请写出图中所有的等边三角形.
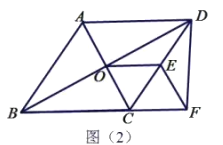
【答案】(1)见解析;(2)![]()
【解析】
(1)根据菱形的性质和三角形中位线的性质可得![]() ,再根据平行四边形的判定和性质可得EF=OC;
,再根据平行四边形的判定和性质可得EF=OC;
(2)由(1)的结论和题意可得![]() 是等边三角形,再由菱形的性质可得OC=
是等边三角形,再由菱形的性质可得OC=![]() AC,从而可得
AC,从而可得![]() 也是等边三角形.
也是等边三角形.
![]() 证明:四边形
证明:四边形![]() 是菱形,
是菱形,![]() ,
,
又∵点E是CD的中点,
![]() ,
,![]()
![]() ,
,
![]() 又,
又,![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ;
;
(2)∵EF=CF,CF=CE,
∴△CEF是等边三角形;
∵四边形![]() 是平行四边形,
是平行四边形,
∴OE=CF,OC=EF,
又∵CE=CF,EF=CF,
∴CE=OE=OC,
△OCE是等边三角形;
∵四边形ABCD是菱形,
∴OC=![]() AC,AD=CD=AB=BC,
AC,AD=CD=AB=BC,
又∵CE=![]() CD,OC=CE,
CD,OC=CE,
∴AC=CD= AD=AB=BC,
∴△ABC,△ACD是等边三角形;
综上所述:图中的等边三角形有:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目