题目内容
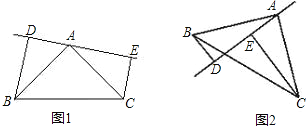
【题目】在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.
小明做了如下操作:
将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:
(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;
(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形.

【答案】(1)四边形ABDF是菱形;理由见解析;(2)证明见解析.
【解析】
试题(1)根旋转的性质得AB=DF,BD=FA,由于AB=BD,所以AB=BD=DF=FA,则可根据菱形的判定方法得到四边形ABDF是菱形;
(2)由于四边形ABDF是菱形,则AB∥DF,且AB=DF,再根据旋转的性质易得四边形ABCE为平行四边形,根据判死刑四边形的性质得AB∥CE,且AB=CE,所以CE∥FD,CE=FD,所以可判断四边形CDEF是平行四边形.
试题解析:(1)解:四边形ABDF是菱形.理由如下:
∵△ABD绕着边AD的中点旋转180°得到△DFA,
∴AB=DF,BD=FA,
∵AB=BD,
∴AB=BD=DF=FA,
∴四边形ABDF是菱形;
(2)证明:∵四边形ABDF是菱形,
∴AB∥DF,且AB=DF,
∵△ABC绕着边AC的中点旋转180°得到△CEA,
∴AB=CE,BC=EA,
∴四边形ABCE为平行四边形,
∴AB∥CE,且AB=CE,
∴CE∥FD,CE=FD,
∴四边形CDEF是平行四边形.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目