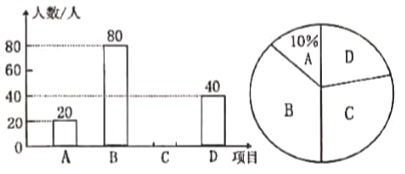
题目内容
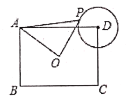
【题目】如图,![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,当点
,当点![]() 、
、![]() 、
、![]() 三点共线时,旋转角为
三点共线时,旋转角为![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,下面结论:①
,下面结论:①![]() 为等腰三角形;②
为等腰三角形;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 中,正确结论的个数是( )
中,正确结论的个数是( )
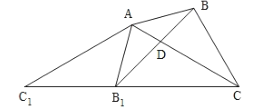
A.2个B.3个C.4个D.5个
【答案】C
【解析】
首先根据旋转性质得出![]() ,从而对结论①进行判断,然后通过对三角形内部角度之间的计算进一步对结论④进行判断,再后通过证明∠
,从而对结论①进行判断,然后通过对三角形内部角度之间的计算进一步对结论④进行判断,再后通过证明∠![]() =∠BDC,∠
=∠BDC,∠![]() =∠BCD对结论②进行判断,再者进一步求出∠
=∠BCD对结论②进行判断,再者进一步求出∠![]() 的度数,由此判断结论③,最后过点D作DM⊥
的度数,由此判断结论③,最后过点D作DM⊥![]() ,通过证明△ABD~△
,通过证明△ABD~△![]() ,利用相似三角形性质进一步分析结论⑤,据此即可得出答案.
,利用相似三角形性质进一步分析结论⑤,据此即可得出答案.
由旋转性质可知:![]() ,
,
∴![]() 为等腰三角形,即①正确;
为等腰三角形,即①正确;
∵∠ACB=30°,
∴∠![]() =∠
=∠![]() =30°,
=30°,
又∵∠![]() =∠BAC=45°,
=∠BAC=45°,
∴∠![]() =75°,
=75°,
∴∠![]() =180°75°30°=75°,
=180°75°30°=75°,
∴CA=![]() ,即④正确;
,即④正确;
∵∠BAC=45°,
∴∠![]() =45°+75°=120°,
=45°+75°=120°,
∵![]() =AB,
=AB,
∴∠![]() =∠ABD=30°,
=∠ABD=30°,
在△![]() 与△BCD中,
与△BCD中,
∵∠![]() =∠BDC,∠
=∠BDC,∠![]() =∠BCD=30°,
=∠BCD=30°,
∴△![]() ~△BCD,即②正确;
~△BCD,即②正确;
∵∠![]() =∠
=∠![]() +∠
+∠![]() =120°,
=120°,
∴旋转角![]() ,即③错误;
,即③错误;
在△ABD与△![]() 中,
中,
∵∠ABD=∠![]() ,∠ADB=∠
,∠ADB=∠![]() ,
,
∴△ABD~△![]() ,
,
∴![]() ,
,
如图,过点D作DM⊥![]() ,
,
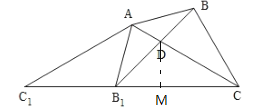
设DM=![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴AC=![]() ,
,
∴AD=![]() ,
,
∴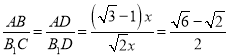 ,即⑤正确;
,即⑤正确;
综上所述,共4个正确,
故选:C.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目