题目内容
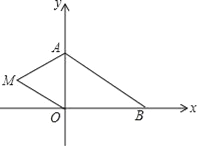
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a﹣2|+(b﹣3)2=0.
(1)求a,b的值;
(2)如果在第二象限内有一点M(m,1),请用含m的式子表示四边形ABOM的面积;
(3)在(2)条件下,当m=﹣![]() 时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
时,在坐标轴的负半轴上是否存在点N,使得四边形ABOM的面积与△ABN的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
【答案】(1)a=2,b=3;
(2)﹣m+3;
(3)N(0,﹣1)或N(﹣1.5,0).
【解析】试题分析:(1)、根据非负数的形状得出a和b的值;(2)、过点M作MN丄y轴于点N,根据四边形的面积等于△AOM和△AOB的和得出答案;(3)、首先根据题意得出面积,然后分点N在x轴的负半轴和y轴的负半轴两种情况分别求出答案.
试题解析:(1)、∵a,b满足|a﹣2|+(b﹣3)2=0, ∴a﹣2=0,b﹣3=0,
解得a=2,b=3;
(2)、过点M作MN丄y轴于点N.
四边形AMOB面积=S△AMO+S△AOB=![]() MNOA+
MNOA+![]() OAOB=
OAOB=![]() ×(﹣m)×2+
×(﹣m)×2+![]() ×2×3=﹣m+3;
×2×3=﹣m+3;
(3)当m=﹣![]() 时,四边形ABOM的面积=4.5. ∴S△ABN=4.5,
时,四边形ABOM的面积=4.5. ∴S△ABN=4.5,
①当N在x轴负半轴上时,
设N(x,0),则S△ABN=![]() AONB=
AONB=![]() ×2×(3﹣x)=4.5, 解得x=﹣1.5;
×2×(3﹣x)=4.5, 解得x=﹣1.5;
②当N在y轴负半轴上时,设N(0,y),则
S△ABN=![]() BOAN=
BOAN=![]() ×3×(2﹣y)=4.5, 解得y=﹣1.
×3×(2﹣y)=4.5, 解得y=﹣1.
∴N(0,﹣1)或N(﹣1.5,0).


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目