题目内容
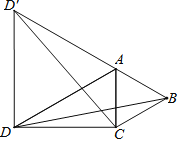
【题目】如图,在△ACD中,AD=9,CD=![]() ,△ABC中,AB=AC,若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′
,△ABC中,AB=AC,若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′
(1)求证:BD=CD′
(2)求BD的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)只要证明△CAD′≌△BAD即可解决问题.
(2)首先证明∠CDD′=90°,利用勾股定理求出CD′,再利用全等三角形的性质即可解决问题.
(1)证明:∵△ADD′和△ABC都是等边三角形,
∴AD=AD′,AC=AB,∠DAD′=∠CAB=60°,
∴∠CAD′=∠BAD,
在△CAD′和△BAD中,
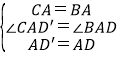 ,
,
∴△CAD′≌△BAD,
∴BD=CD′.
(2)解:∵△ADD′是等边三角形,
∴∠ADD′=60°,DD′=AD=9,
∵∠ADC=30°,
∴∠CDD′=90°,
∴CD′=![]() ,
,
∵△CAD′≌△BAD,
∴BD=CD′=3![]() .
.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目