��Ŀ����
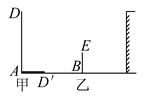
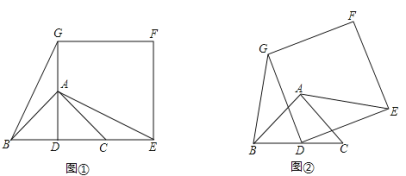
����Ŀ����ͼ(1)����֪��ABC�ǵ���ֱ�������Σ���BAC��90������D��BC���е㣮��������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG��
��1���Բ����߶�BG��AE�Ĺ�ϵ(λ�ù�ϵ��������ϵ)����ֱ��д����õ��Ľ��ۣ�
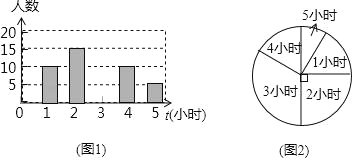
��2����������DEFG�Ƶ�D��ʱ�뷽����תһ�Ƕ�����(0��������90��)����ͼ(2)��ͨ���۲������ȷ����ж�(1)�еĽ����Ƿ���Ȼ���������������������֤�����������������˵�����ɣ�
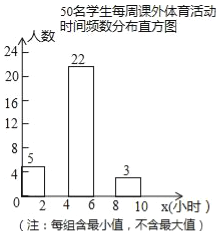
��3����BC��DE��2��������DEFG�Ƶ�D��ʱ�뷽����ת�Ƕ��� (0��������360��)�����У���BGΪ��Сֵʱ����AF��ֵ��
���𰸡���1������Ҵ�ֱ����2������������������3��![]() .
.
��������
��1���������õ���ֱ�������ε����ʺ������ε����ʵó�DG=DE��AD=BD�������ó���BDG�ա�ADE�����ɵó��𰸣�
��2���ӳ�EA�ֱ�DG��BG�ڵ�N��M���㣬����֤����BDG�ա�ADE�������ó�BG��AE��BG=AE��
��3���ɣ�2��֪��ҪʹAE���ֻҪ���������Ƶ�D��ʱ������ת270������A��D��E��һ��ֱ����ʱ��AE�����������ɣ�
�⣺��1����ͼ��1��
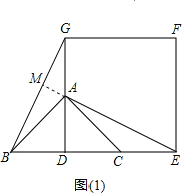
�ߡ�ABC�ǵ���ֱ�������Σ���BAC=90������D��BC���е㣬
��BD=CD=AD��
������BDG����ADE��
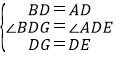
���BDG�ա�ADE��SAS����
��BG=AE����DGB=��DEA��
�ӳ�EA��BG��һ��M��
���GAM=��DAE��
���GMA=��EDA=90����
���߶�BG��AE����Ҵ�ֱ��
��2��������
��ͼ��2�����ӳ�EA�ֱ�DG��BG�ڵ�M����N�����㣬
�ߡ�ABC�ǵ���ֱ�������Σ���BAC=90������D��BC���е㣬
���ADB=90������BD=AD��
�ߡ�BDG=��ADB-��ADG=90��-��ADG=��ADE��
������BDG����ADE��
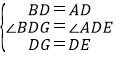
���BDG�ա�ADE��SAS����
��BG=AE����DEA=��DGB��
�ߡ�DEA+��DNE=90������DNE=��MNG��
���MNG+��DGM=90����
��BG��AE��BG=AE��
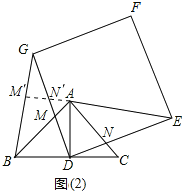
��3���ɣ�2��֪��ҪʹAE���ֻҪ���������Ƶ�D��ʱ������ת270������A��D��E��һ��ֱ����ʱ��AE���
��������DEFG���Ƶ�D��ת�Ĺ����У�E���˶���ͼ�����Ե�DΪԲ�ģ�DEΪ�뾶��Բ��
�൱������DEFG��ת��G��λ��BC���ӳ����ϣ���������DEFG�Ƶ�D��ʱ�뷽����ת270����ʱ��BG�����ͼ��3����
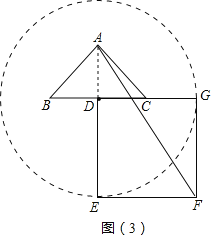
��BC=DE=m����AD=![]() ��EF=m��
��EF=m��
��Rt��AEF��AF2=AE2+EF2=��AD+DE��2+EF2=![]()
��AF=![]() ������������DEFG��ת�����У���AEΪ���ֵʱ��AF=
������������DEFG��ת�����У���AEΪ���ֵʱ��AF=![]() .
.

 ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д� �㽭֮�ǿ�ʱ�Ż���ҵϵ�д�
�㽭֮�ǿ�ʱ�Ż���ҵϵ�д� ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д�