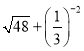ЬтФПФкШн
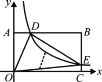
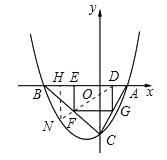
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊХзЮяЯпPЃКyЃНax2ЃЋbxЃЋc(aЁй0)гыxжсНЛгкAЃЌBСНЕу(ЕуAдкxжсЕФе§АыжсЩЯ)ЃЌгыyжсНЛгкЕуCЃЌОиаЮDEFGЕФвЛЬѕБпDEдкЯпЖЮABЩЯЃЌЖЅЕуFЃЌGЗжБ№дкЯпЖЮBCЃЌACЩЯЃЌХзЮяЯпPЩЯЕФВПЗжЕуЕФКсзјБъЖдгІЕФзнзјБъШчЯТ.

(1)ЧѓAЃЌBЃЌCШ§ЕуЕФзјБъЃЛ
(2)ШєЕуDЕФзјБъЮЊ(mЃЌ0)ЃЌОиаЮDEFGЕФУцЛ§ЮЊSЃЌЧѓSгыmЕФКЏЪ§ЙиЯЕЪНЃЌВЂжИГіmЕФШЁжЕЗЖЮЇЃЛ
(3)ЕБОиаЮDEFGЕФУцЛ§SзюДѓЪБЃЌСЌНгDFВЂбгГЄжСЕуMЃЌЪЙFMЃНkЁЄDFЃЌШєЕуMВЛдкХзЮяЯпPЩЯЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
(4)ШєЕуDЕФзјБъЮЊ(1ЃЌ0)ЃЌЧѓОиаЮDEFGЕФУцЛ§ЃЎ
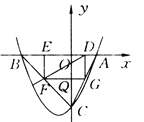
ЁОД№АИЁПЃЈ1ЃЉA(2ЃЌ0)ЃЌB(Ѓ4ЃЌ0)ЃЌC(0ЃЌЃ4)ЃЛЃЈ2ЃЉSОиаЮDEFG=12mЃ6m2(0ЃМmЃМ2)ЃЛЃЈ3ЃЉkЕФШЁжЕЗЖЮЇЪЧkЁй![]() ЧвkЃО0ЃЛЃЈ4ЃЉSОиаЮDEFGЃН6ЃЎ
ЧвkЃО0ЃЛЃЈ4ЃЉSОиаЮDEFGЃН6ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉПЩШЮбЁШ§зщзјБъЃЌгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіХзЮяЯпPЕФНтЮіЪНЃЎШЛКѓИљОнХзЮяЯпPЕФНтЮіЪНМДПЩЕУГіAЁЂBЁЂCШ§ЕуЕФзјБъЃЛ
ЃЈ2ЃЉЧѓОиаЮЕФУцЛ§ашжЊЕРОиаЮЕФГЄКЭПэЃЌПЩЯШдкжБНЧШ§НЧаЮAOCжаЃЌИљОнADЃЌOAЃЌDGЃЌCDЕФБШР§ЙиЯЕЪНЃЌгУmБэЪОГіDGЕФГЄЃЌЭЌРэПЩдкжБНЧШ§НЧаЮBCOжаБэЪОГіOEЕФГЄЃЌНјЖјПЩИљОнED=EO+ODЕУГіEDЕФГЄЃЌШЛКѓгЩОиаЮЕФУцЛ§ЙЋЪНМДПЩЕУГіSгыmЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉЕФКЏЪ§ЙиЯЕЪНМДПЩЕУГіSЕФзюДѓжЕМАЖдгІЕФmЕФжЕЃЎНјЖјПЩЕУГіDЃЌEЃЌFЃЌGЕФзјБъЃЎШчЙћЩшDFЕФбгГЄЯпНЛХзЮяЯпгкNЕуЃЌФЧУДПЩЯШЧѓГіFNгыDFЕФБШР§ЙиЯЕЃЎШчЙћЙ§NзїxжсЕФДЙЯпЩшДЙзуЮЊHЃЌФЧУДЮвУЧПЩЕУГіEFЃКDF=DFЃКDNЃЌЖјEFЃЌDFОљЮЊFЃЌNЕуЕФзнзјБъЕФОјЖджЕЃЌвђДЫвЊЯШЧѓГіNЕуЕФзнзјБъЃЌПЩЯШИљОнDЁЂFЕФзјБъЧѓГіжБЯпDFЕФНтЮіЪНЃЌШЛКѓСЊСЂжБЯпDFЕФНтЮіЪНгыХзЮяЯпPЕФНтЮіЪНЧѓГіNЕуЕФзјБъЃЌШЛКѓИљОнЩЯЪіБШР§ЙиЯЕЧѓГіFNЁЂDFЕФБШР§ЙиЯЕЃЌШчЙћЧѓГіДЫЪБFN=k1DFЃЌФЧУДгЩгкMВЛдкХзЮяЯпЩЯЃЌвђДЫkЕФШЁжЕЗЖЮЇОЭЪЧkЃО0ЃЌЧвkЁйk1ЃЎ
ЃЈ4ЃЉгЩ![]() ЃЌAD=1ЃЌAO=2ЃЌOC=4ЃЌЕУЕНDG=2ЃЎгжгЩ
ЃЌAD=1ЃЌAO=2ЃЌOC=4ЃЌЕУЕНDG=2ЃЎгжгЩ![]() ЃЌAB=6ЃЌCP=2ЃЌOC=4ЃЌЕУЕНFG=3ЃЌДгЖјЕУЕННсТлЃЎ
ЃЌAB=6ЃЌCP=2ЃЌOC=4ЃЌЕУЕНFG=3ЃЌДгЖјЕУЕННсТлЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЩшy=ax2+bx+cЃЈaЁй0ЃЉЃЌШЮШЁxЃЌyЕФШ§зщжЕДњШыЃЌЕУЃК 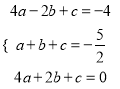 ЃЌНтЕУЃК
ЃЌНтЕУЃК 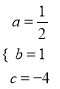 ЃЌЁрНтЮіЪНЮЊЃК
ЃЌЁрНтЮіЪНЮЊЃК ![]() ЃЌСюy=0ЃЌНтЕУx1=Љ4ЃЌx2=2ЃЛ
ЃЌСюy=0ЃЌНтЕУx1=Љ4ЃЌx2=2ЃЛ
Сюx=0ЃЌЕУy=Љ4ЃЌЁрAЁЂBЁЂCШ§ЕуЕФзјБъЗжБ№ЪЧAЃЈ2ЃЌ0ЃЉЃЌBЃЈЉ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ4ЃЉЃЎ
ЃЈ2ЃЉгЩЬтвтЕУЃК ![]() ЃЌЖјAO=2ЃЌOC=4ЃЌAD=2ЉmЃЌЙЪDG=4Љ2mЃЌгж
ЃЌЖјAO=2ЃЌOC=4ЃЌAD=2ЉmЃЌЙЪDG=4Љ2mЃЌгж![]() ЃЌEF=DGЃЌЕУBE=4Љ2mЃЌЁрDE=3mЃЌЁрSDEFG=DGDE=ЃЈ4Љ2mЃЉ3m=12mЉ6m2ЃЈ0ЃМmЃМ2ЃЉЃЎ
ЃЌEF=DGЃЌЕУBE=4Љ2mЃЌЁрDE=3mЃЌЁрSDEFG=DGDE=ЃЈ4Љ2mЃЉ3m=12mЉ6m2ЃЈ0ЃМmЃМ2ЃЉЃЎ
ЃЈ3ЃЉЁпSDEFG=Љ6m2+12m=Љ6ЃЈmЉ1ЃЉ2+6ЃЌЃЈ0ЃМmЃМ2ЃЉЃЌЁрm=1ЪБЃЌОиаЮЕФУцЛ§зюДѓЃЌЧвзюДѓУцЛ§ЪЧ6ЃЎ
ЕБОиаЮУцЛ§зюДѓЪБЃЌЦфЖЅЕуЮЊDЃЈ1ЃЌ0ЃЉЃЌGЃЈ1ЃЌЉ2ЃЉЃЌFЃЈЉ2ЃЌЉ2ЃЉЃЌEЃЈЉ2ЃЌ0ЃЉЁЃЩшжБЯпDFЕФНтЮіЪНЮЊy=kx+bЃЌвзжЊЃЌk=![]() ЃЌb=Љ
ЃЌb=Љ![]() ЃЌЁр
ЃЌЁр![]() ЁЃгжвђЮЊХзЮяЯпPЕФНтЮіЪНЮЊЃК
ЁЃгжвђЮЊХзЮяЯпPЕФНтЮіЪНЮЊЃК ![]() ЃЌСю
ЃЌСю![]() ЃЌНтЕУЃКx=
ЃЌНтЕУЃКx=![]() ЃЎ
ЃЎ
ЩшЩфЯпDFгыХзЮяЯпPЯрНЛгкЕуNЃЌдђNЕФКсзјБъЮЊ![]() ЃЌЙ§NзїxжсЕФДЙЯпНЛxжсгкHЃЌга
ЃЌЙ§NзїxжсЕФДЙЯпНЛxжсгкHЃЌга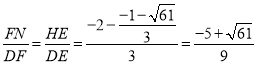 ЃЌЕуMВЛдкХзЮяЯпPЩЯЃЌМДЕуMВЛгыNжиКЯЪБЃЌДЫЪБkЕФШЁжЕЗЖЮЇЪЧkЁй
ЃЌЕуMВЛдкХзЮяЯпPЩЯЃЌМДЕуMВЛгыNжиКЯЪБЃЌДЫЪБkЕФШЁжЕЗЖЮЇЪЧkЁй![]() ЧвkЃО0ЃЎ
ЧвkЃО0ЃЎ
ЃЈ4ЃЉЁп![]() ЃЌЖјAD=1ЃЌAO=2ЃЌOC=4ЃЌдђDG=2ЃЎгжЁп
ЃЌЖјAD=1ЃЌAO=2ЃЌOC=4ЃЌдђDG=2ЃЎгжЁп![]() ЃЌЖјAB=6ЃЌCP=2ЃЌOC=4ЃЌдђFG=3ЃЌЁрSDEFG=DGFG=6ЃЎ
ЃЌЖјAB=6ЃЌCP=2ЃЌOC=4ЃЌдђFG=3ЃЌЁрSDEFG=DGFG=6ЃЎ

 аТБраЁбЇЕЅдЊздВтЬтЯЕСаД№АИ
аТБраЁбЇЕЅдЊздВтЬтЯЕСаД№АИ зжДЪОфЖЮЦЊЯЕСаД№АИ
зжДЪОфЖЮЦЊЯЕСаД№АИЁОЬтФПЁП2013Фъ3дТ28ШеЪЧШЋЙњжааЁбЇЩњАВШЋНЬг§ШеЃЌФГбЇаЃЮЊМгЧПбЇЩњЕФАВШЋвтЪЖЃЌзщжЏСЫШЋаЃ1500УћбЇЩњВЮМгАВШЋжЊЪЖОКШќЃЌДгжаГщШЁСЫВПЗжбЇЩњГЩМЈЃЈЕУЗжШЁе§ећЪ§ЃЌТњЗжЮЊ100ЗжЃЉНјааЭГМЦЃЌЧыИљОнЩаЮДЭъГЩЕФЦЕТЪЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЃЌНтД№ЯТСаЮЪЬтЃК
ЦЕТЪЗжВМБэ
ЗжЪ§ЖЮ | ЦЕЪ§ | ЦЕТЪ |
50.5ЁЋ60.5 | 16 | 0.08 |
60.5ЁЋ70.5 | 40 | 0.2 |
70.5ЁЋ80.5 | 50 | 0.25 |
80.5ЁЋ90.5 | m | 0.5 |
90.5ЁЋ100.5 | 24 | n |

ЃЈЃБЃЉетДЮГщШЁСЫ УћбЇЩњЕФОКШќГЩМЈНјааЭГМЦЃЌЦфжаЃКm= ЃЌn ЃЛ
ЃЈЃВЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈЃГЃЉШєГЩМЈдк70ЗжвдЯТЃЈКЌ70ЗжЃЉЕФбЇЩњЮЊАВШЋвтЪЖВЛЧПЃЌгаД§НјвЛВНМгЧПАВШЋНЬг§ЃЌдђИУаЃАВШЋвтЪЖВЛЧПЕФбЇЩњдМгаЖрЩйШЫЃП