题目内容
武汉市某中学标准化建设规划在校园内的一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草(如图所示),若使每一块草坪的面积都为96平方米,设人行道的宽为x米,下列方程:
①(36-2x)(20-x)=96×6
②2×20x+(36-2x)x=36×20-96×6
③(18-x)(10- )=
)= ×96×6
×96×6
其中正确的个数为
- A.0个
- B.1个
- C.2个
- D.3个
D
分析:六块草坪组合到一起,正好构成一个矩形,根据这矩形的面积,设人行道的宽为x米,则矩形的长是(36-2x)m,宽是(20-x)m,即可得到方程①(36-2x)(20-x)=96×6;
根据六块草坪的面积的和等于矩形场地的面积-路的面积,即可列出方程2×20x+(36-2x)x=36×20-96×6;
将方程①两边同除4可得:(18x-x)(10- )=
)= ×96×6.
×96×6.
解答:依题意得可列出方程①、(36-2x)(20-x)=96×6;
②、20x×2+36×x+96×6=36×20;即2×20x+(36-2x)x=36×20-96×6;
③、将方程①两边同除4可得:(18x-x)(10- )=
)= ×96×6;
×96×6;
∴正确的为①、②、③,
故选D.
点评:一元二次方程的运用,此类题是看准题型列出方程,题目不难,重在看准题;每一块草坪的面积=草坪的长×草坪的宽.
分析:六块草坪组合到一起,正好构成一个矩形,根据这矩形的面积,设人行道的宽为x米,则矩形的长是(36-2x)m,宽是(20-x)m,即可得到方程①(36-2x)(20-x)=96×6;
根据六块草坪的面积的和等于矩形场地的面积-路的面积,即可列出方程2×20x+(36-2x)x=36×20-96×6;
将方程①两边同除4可得:(18x-x)(10-
 )=
)= ×96×6.
×96×6.解答:依题意得可列出方程①、(36-2x)(20-x)=96×6;
②、20x×2+36×x+96×6=36×20;即2×20x+(36-2x)x=36×20-96×6;
③、将方程①两边同除4可得:(18x-x)(10-
 )=
)= ×96×6;
×96×6;∴正确的为①、②、③,
故选D.
点评:一元二次方程的运用,此类题是看准题型列出方程,题目不难,重在看准题;每一块草坪的面积=草坪的长×草坪的宽.

练习册系列答案
相关题目
 上,则下列各点不在双曲线上的是
上,则下列各点不在双曲线上的是 如图所示,OM是∠BOC的角平分线,ON是∠AOB的角平分线,且∠AOC=72°,试求∠MON的度数.当OB在∠AOC内取不同位置时,∠MON的值是否发生变化?并说明理由.
如图所示,OM是∠BOC的角平分线,ON是∠AOB的角平分线,且∠AOC=72°,试求∠MON的度数.当OB在∠AOC内取不同位置时,∠MON的值是否发生变化?并说明理由. 如图,已知DE∥BC,AD=5,DB=3,BC=9.9,∠B=50°,则∠ADE=________度,DE=________,
如图,已知DE∥BC,AD=5,DB=3,BC=9.9,∠B=50°,则∠ADE=________度,DE=________,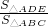 =________.
=________.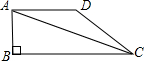 如图,在直角梯形ABCD中,已知AB=3,AD=CD=5,则对角线AC的长为________.
如图,在直角梯形ABCD中,已知AB=3,AD=CD=5,则对角线AC的长为________.