题目内容
已知二次函数y=ax2+bx+c的图象与x轴交于(x1,0)、(x2,0)两点,且0<x1<1,1<x2<2,与轴y交于点(0,-2).下列结论:①2a+b>1;②3a+b>0;③a-b<2;④a<-1.其中正确结论的个数为( )
| A.4 | B.3 | C.2 | D.1 |
如图:
0<x1<1,1<x2<2,并且图象与y轴相交于点(0,-2),
可知该抛物线开口向下即a<0,c=-2,
①当x=2时,y=4a+2b+c<0,即4a+2b<-c;
∵c=-2,
∴4a+2b<2,
∴2a+b<1,
故本选项错误;
②∵0<x1<1,1<x2<2,
∴1<x1+x2<3,
又∵x1+x2=-
,
∴1<-
<3,
∴3a+b<0,
故本选项错误;
③当x=-1时,y=a-b+c<0,
∵c=-2,
∴a-b<-c,
即a-b<2,
故本选项正确;
④∵0<x1x2<2,x1x2=
<2,
又∵c=-2,
∴a<-1.
故本选项正确.
故选C.
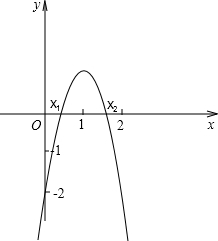
0<x1<1,1<x2<2,并且图象与y轴相交于点(0,-2),
可知该抛物线开口向下即a<0,c=-2,
①当x=2时,y=4a+2b+c<0,即4a+2b<-c;
∵c=-2,
∴4a+2b<2,
∴2a+b<1,
故本选项错误;
②∵0<x1<1,1<x2<2,
∴1<x1+x2<3,
又∵x1+x2=-
| b |
| a |
∴1<-
| b |
| a |
∴3a+b<0,
故本选项错误;
③当x=-1时,y=a-b+c<0,
∵c=-2,
∴a-b<-c,
即a-b<2,
故本选项正确;
④∵0<x1x2<2,x1x2=
| c |
| a |
又∵c=-2,
∴a<-1.
故本选项正确.
故选C.


练习册系列答案
相关题目
