题目内容
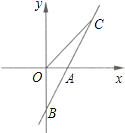
【题目】如图，在平面直角坐标系中， A（-1,0），B（3,0），C（0,2），CD∥x轴，CD=AB．
(1)求点D的坐标
（2）四边形OCDB的面积
(3)在y轴上是否存在一点P，使
＝
，若存在这样一点，求出点P的坐标，若不存在，试说明理由．
【答案】（1）D（4,2）；（2）7；（3）存在，P（0， 
）或（0， 
）
【解析】试题分析：（1）依题意知，将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，故C、D两点点y值为2. 所以可求点D的坐标；
（2）结合图形，根据梯形的面积公式求解；
（3）通过面积相等法，直接根据三角形的面积和四边形的面积可求解.
试题解析：（1）∵A（-1,0），B（3,0）
∴AB=4
∵CD=AB
∴CD=4
∵C（0,2），CD∥x轴
∴D（4,2）
（2）
=7
（3）存在，理由如下
设P（0，y）
∵
＝
∴
∴
∴
∴P（0， 
）或（0， 
）
练习册系列答案
全优点练单元计划系列答案
相关题目
