题目内容
半径分别为r1，r2的⊙O1和⊙O2相离，并且一条外公切线长度为t1，一条内公切线的长度为t2，则t12-t22=分析：连接O1A，O1C，O2B，O2D作O2E⊥O1A于E，延长O1E到F使CF=O2D=r2，连接O2F，根据直角三角形中三边长度即可求得锐角的三角函数值，即可解题．
解答：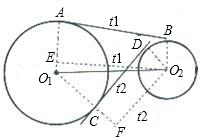
解：如图，连接O1A，O1C，O2B，O2D，
作O2E⊥O1A于E，延长O1E到F使CF=O2D=r2，连接O2F，
则∠EO2O1=α，∠FO2O1=β
∴sinα=
，sinβ=
，
在Rt△EO1O2中，t12=O1O22-（r1-r2）2①
在Rt△O1FO2中，t22=O1O22-（r1+r2）2②
①-②得t12-t22=4r1r2，
故答案为4、
、
．
解：如图，连接O1A，O1C，O2B，O2D，作O2E⊥O1A于E，延长O1E到F使CF=O2D=r2，连接O2F，
则∠EO2O1=α，∠FO2O1=β
∴sinα=
| |r1-r2| |
| o1o2 |
| r1+r2 |
| o1o2 |
在Rt△EO1O2中，t12=O1O22-（r1-r2）2①
在Rt△O1FO2中，t22=O1O22-（r1+r2）2②
①-②得t12-t22=4r1r2，
故答案为4、
| |r1-r2| |
| o1o2 |
| r1+r2 |
| o1o2 |
点评：本题考查了三角函数值的求值，考查了直角三角形中三角函数值的应用，考查了勾股定理在直角三角形中的运用．
练习册系列答案
相关题目
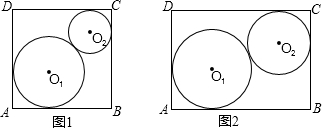
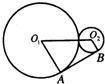
8、如图，半径分别为r1，r2的⊙O1、⊙O2相外切，AB为两圆的外公切线，O1O2为连心线，若∠AO1O2=60°，r1=6，则r2等于（ ）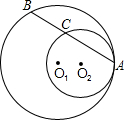
如图，⊙O1与⊙O2内切于点A，其半径分别为r1与r2（r1＞r2）．若⊙O1的弦AB交⊙O2于点C（O1不在AB上），则AB：AC的值等于（ ）