Question

【题目】如图，是等腰直角三角形，，点是直线上的一个动点（点与点不重合），以为腰作等腰直角，连接.

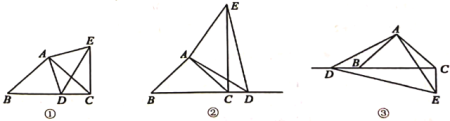
（1）如图①，当点在线段上时，直接写出的位置关系，线段，之间的数量关系；

（2）如图②，当点在线段的延长线上时，试判断线段，的位置关系，线段之间的数量关系，并说明理由；

（3）如图③，当点在线段的延长线上时，试判断线段的位置关系，线段之间的数量关系，并说明理由.

Answer 1

【答案】（1）见解析；（2），，理由见解析；（3），理由见解析

【解析】

（1）根据条件AB=AC，∠BAC=90°，AD=AE，∠DAE=90°，判定△ABD≌△ACE（SAS），利用两角的和即可得出；利用线段的和差即可得出；
（2）同（1）的方法根据SAS证明△ABD≌△ACE，得出BD=CE，∠ACE=∠ABD，从而得出结论；
（3）先根据SAS证明△ABD≌△ACE，得出，，从而得出结论．

（1）∵△ABC、△ADE是等腰直角三角形，

∴AB＝AC，AE＝AD，

在△△ABD和△ACE中

，

∴△ABD≌△ACE（SAS），

∴∠B＝∠ACE，BD=CE,

又∵△ABC是等腰直角三角形，

∴∠B+∠ACB=,

∴∠ACE +∠ACB=,即，

∵BC=BD+CD, BD=CE，

∴；

（2），，理由如下：

∵、是等腰直角三角形，

∴，

∴

即,

在和中

∴

∴

∵

∴，

∴，

∵

∴

∴.

（3），理由如下：

∵是等腰直角三角形，

∴，

∴，即，

在和中

∴，

∴，，

∵，

∴，

∵，即

∴，

∴，即.