题目内容
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC.MN是过点A的直线,BD⊥MN 于D,CE⊥MN于E.
(1)求证:BD=AE.
(2)若将MN绕点A旋转,使MN与BC相交于点G(如图2),其他条件不变,求证:BD=AE.
(3)在(2)的情况下,若CE的延长线过AB的中点F(如图3),连接GF,求证:∠AFE=∠BFG.

【答案】(1)证明见详解;(2)证明见详解;(3)证明见详解.
【解析】
(1)首先证明∠1=∠3,再证明△ADB≌△CEA,然后根据全等三角形的性质可得BD=AE;
(2)首先证明∠BAD=∠ACE,再证明△ABD≌△CAE,根据全等三角形对应边相等可得BD=AE;
(3)首先证明△ACF≌△BAP,然后再证明△BFG≌△BPG,再根据全等三角形对应角相等可得∠BPG=∠BFG,再根据等量代换可得结论∠BFG=∠AFE.
证明:(1)如图,
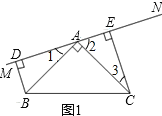
∵BD⊥MN,CE⊥MN,
∴∠BDA=∠AEC=90°,
∵∠BAC=90°,
∴∠1+∠2=90°,
又∵∠3+∠2=90°,
∴∠1=∠3,
在△ADB和△CEA中, ,
,
∴△ADB≌△CEA(AAS),
∴BD=AE;
(2)如图,

∵BD⊥MN,CE⊥MN,
∴∠BDA=∠CEA=90°,
∵∠BAD+∠CAE=90°,∠ACE+∠CAE=90°,
∴∠BAD=∠ACE,
在△ABD和△CAE中,

∴△ABD≌△CAE(AAS),
∴BD=AE;
(3)过B作BP∥AC交MN于P,
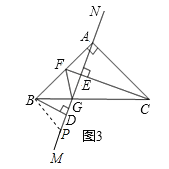
∵BP∥AC,
∴∠PBA+∠BAC=180°,
∵∠BAC=90°,
∴∠PBA=∠BAC=90°,
由(2)得:∠BAP=∠ACF,
∴在△ACF和△BAP中,
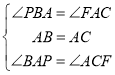
∴△ACF≌△BAP(ASA),
∴∠AFC=∠BPA,AF=BP
∵BF=AF,
∴BF=BP,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
又∵∠PBA=90°,
∴∠PBG=45°,
∴∠ABC=∠PBG,
在△BFG和△BPG中,
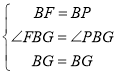
∴△BFG≌△BPG(SAS),
∴∠BPG=∠BFG,
∵∠BPG=∠AFE,
∴∠BFG=∠AFE.

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案【题目】行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号的汽车的刹车性能(车速不超过140 km/h),对这种汽车进行测试,测得数据如下表:
刹车时车速/km·h-1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
刹车距离/m | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
(1)以车速为x轴,以刹车距离为y轴,建立平面直角坐标系,根据上表对应值作出函数的大致图象;
(2)观察图象.估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道发生了一次交通事故,现场测得刹车距离为46.5 m,推测刹车时的车速是多少?请问事故发生时,汽车是超速行驶还是正常行驶?






