题目内容
(2006•玉溪)如图,轴对称图形ABCDEFG的面积为56,∠A=90°,则点D的坐标是( )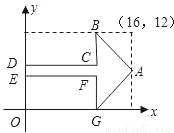
A.(0,6)
B.(0,6.5)
C.(0,7)
D.(0,7.5)
【答案】分析:根据等腰直角三角形的性质求出△ABG的面积,得出矩形CDEF的面积,从而求出DE的长,结合轴对称的基本性质得到点D的坐标.
解答: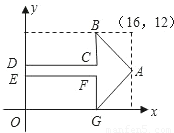 解:∵这是一个轴对称图形,
解:∵这是一个轴对称图形,
∴A点坐标为(16,6).
又∵∠A=90°,
∴△ABG是等腰直角三角形,
∴AB=AG=6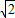
∴△ABG的面积为 AB•AG=
AB•AG= ×6
×6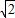 ×6
×6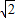 =36,
=36,
所以矩形CDEF的面积为20,
又∵EF=16-6=10,
∴DE=2,
所以D点坐标为(0,7).
故选D.
点评:此题考查轴对称的基本性质,结合了图形的常见的变化,要根据等腰直角三角形的性质求出边长;此题考查的计算技巧性很强,要注意对一些特殊三角形的性质的应用.
解答:
 解:∵这是一个轴对称图形,
解:∵这是一个轴对称图形,∴A点坐标为(16,6).
又∵∠A=90°,
∴△ABG是等腰直角三角形,
∴AB=AG=6
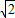
∴△ABG的面积为
 AB•AG=
AB•AG= ×6
×6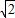 ×6
×6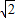 =36,
=36,所以矩形CDEF的面积为20,
又∵EF=16-6=10,
∴DE=2,
所以D点坐标为(0,7).
故选D.
点评:此题考查轴对称的基本性质,结合了图形的常见的变化,要根据等腰直角三角形的性质求出边长;此题考查的计算技巧性很强,要注意对一些特殊三角形的性质的应用.

练习册系列答案
相关题目