题目内容
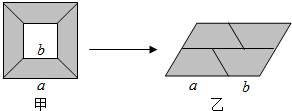
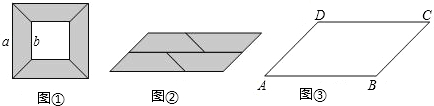
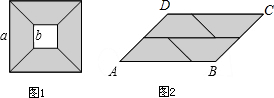
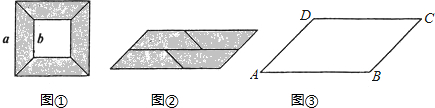
从边长为a的大正方形纸板中间挖去一个边长为b的小正方形后,将其截成四个相同的等腰梯形﹙如图1﹚,可以拼成一个平行四边形ABCD﹙如图2﹚.已知∠A=45°,AB=8,AD=4 .则原来的大正方形的面积为________.
.则原来的大正方形的面积为________.
36
分析:过Q作QT⊥AE于T,FH⊥AE于H,推出平行四边形QTHF,求出AT、QT,根据勾股定理求出AQ,根据题意得到方程组,求出方程组的解即可.
解答: 解:过Q作QT⊥AE于T,FH⊥AE于H,
解:过Q作QT⊥AE于T,FH⊥AE于H,
∵QF∥AE,QT∥FH,
∴四边形QTHF是平行四边形,
∴QF=TH=a-b,
∵∠A=45°,∠ATQ=90°,
∴AT=HE=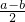 ,
,
∴QT=AT=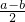 ,
,
在△ATQ中由勾股定理得:AQ= ,
,
根据题意得:AB=a+b=8,
AD=2× =4
=4 ,
,
解得:a=6,
∴a2=36.
故答案为:36.
点评:本题主要考查对等腰梯形的性质,平行四边形的性质和判定,解二元一次方程组,勾股定理,正方形的性质等知识点的理解和掌握,能综合运用性质进行推理是解此题的关键.
分析:过Q作QT⊥AE于T,FH⊥AE于H,推出平行四边形QTHF,求出AT、QT,根据勾股定理求出AQ,根据题意得到方程组,求出方程组的解即可.
解答:
 解:过Q作QT⊥AE于T,FH⊥AE于H,
解:过Q作QT⊥AE于T,FH⊥AE于H,∵QF∥AE,QT∥FH,
∴四边形QTHF是平行四边形,
∴QF=TH=a-b,
∵∠A=45°,∠ATQ=90°,
∴AT=HE=
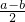 ,
,∴QT=AT=
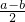 ,
,在△ATQ中由勾股定理得:AQ=
 ,
,根据题意得:AB=a+b=8,
AD=2×
 =4
=4 ,
,解得:a=6,
∴a2=36.
故答案为:36.
点评:本题主要考查对等腰梯形的性质,平行四边形的性质和判定,解二元一次方程组,勾股定理,正方形的性质等知识点的理解和掌握,能综合运用性质进行推理是解此题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目