题目内容
在课外小组活动时,小慧拿来一道题(原问题)和小东、小明交流。
原问题:如图(1),已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB、BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F探究线段DF与EF的数量关系。
小慧同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解;
小东同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°;
小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况,请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
原问题:如图(1),已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB、BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F探究线段DF与EF的数量关系。
小慧同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解;
小东同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°;
小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况,请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
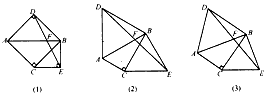
(1)写出原问题中DF与EF的数量关系;
(2)如图(2),若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
(3)如图(3),若∠ADB=∠BEC=2∠ABC,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明。
(2)如图(2),若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
(3)如图(3),若∠ADB=∠BEC=2∠ABC,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明。
| 解:(1)DF=EF; | |
| (2)猜想:DF=FE; 证明:如图(1)所示,过点D作DG⊥AB于G,则∠DGB=90° ∵DA=DB,∠ADB=60°, ∴AG=BC,△DBA是等边三角形, ∴DB=BA, ∵∠ACB=90°,∠ABC=30° ∴AC=1/2AB=BG, ∴△DBG≌△BAC, ∴DG=BC, ∵BE=EC,∠BEC=60°, ∴△EBC是等边三角形, ∴BC=BE,∠CBE=60°, ∴DG=BE,∠ABE=∠ABC+∠CBE=90°, ∵∠DFC=∠EFB,∠DCF=∠EBF, ∴△DFC≌△EFB, ∴DF=EF; |
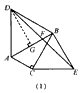 |
| (3)猜想:DF=FE; 如图(2)所示,过点D作DH⊥AB于H,连接HC,HE,HE交CB于K,则∠DHB=90°, ∵DA=DB, ∴AH=BH,∠1=∠HDB, ∵∠ACB=90°, ∴HC=HB, ∵EB=EC,HE=HE, ∴△HBE≌△HCE, ∴∠2=∠3,∠4=∠BEH, ∴HK⊥BC, ∴∠BKE=90°, ∵∠ADB=∠BEC=2∠ABC, ∴∠HDB=∠BEH=∠ABC, ∴∠DBC=∠DBH+∠ABC=∠DBH+∠HDB=90°, ∠EBH=∠EBK+∠ABC=∠EBK+∠BEK=90°, ∴DB∥HE,DH∥BE, ∴四边形DHEB是平行四边形, ∴BF=EF。 |
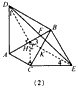 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
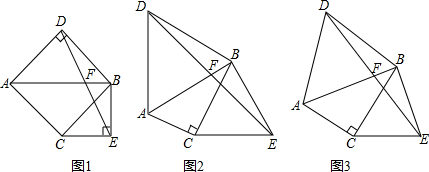 你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.


