题目内容
（2012•西城区模拟）探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（1）完成下列空格：
当已知矩形A的边长分别为6和1时，小明是这样研究的：设所求矩形的一边是x，则另一边为（
| 7 |
| 2 |
| 7 |
| 2 |
∵b2-4ac=49-48＞0，∴x1=
2
2
，x2=| 3 |
| 2 |
| 3 |
| 2 |
∴满足要求的矩形B存在．
小红的做法是：设所求矩形的两边分别是x和y，由题意得方程组：
|
（2）如果已知矩形A的边长分别为2和1，请你仿照小明或小红的方法研究是否存在满足要求的矩形B．
（3）在小红的做法中，我们可以把方程组整理为：
|
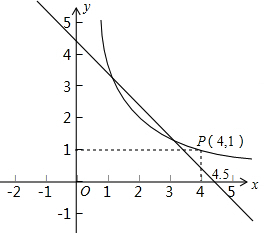
①这个图象所研究的矩形A的面积为
8
8
；周长为18
18
．②满足条件的矩形B的两边长为
9+
| ||
| 4 |
9+
| ||
| 4 |
9-
| ||
| 4 |
9-
| ||
| 4 |
分析：（1）用解一元二次方程的方法求一元二次方程的根即可；
（2）设所求矩形的两边分别是x和y，由题意得方程组，消去y化简再根据方程的判别式解答即可；
（3）①由图可知，一次函数解析式为y=-x+4.5，反比例函数解析式为y=
，组成方程组，消去y求出方程的根，再根据一元二次方程根与系数的关系求出x1+x2=4.5，x1x2=4，即可．
②利用解二元二次方程，可求出满足条件的矩形B的两边长．
（2）设所求矩形的两边分别是x和y，由题意得方程组，消去y化简再根据方程的判别式解答即可；
（3）①由图可知，一次函数解析式为y=-x+4.5，反比例函数解析式为y=
| 4 |
| x |
②利用解二元二次方程，可求出满足条件的矩形B的两边长．
解答：解：（1）x1=2，x2=
，…（4分）
（2）设所求矩形的一边是x，则另一边为（
-x），
由题意得方程：x（
-x）=1，
化简得：2x2-3x+2=0
∵b2-4ac=9-16＜0，
∴原方程无解．
∴满足要求的矩形B不存在．…（8分）
（3）（每空1分）
①由图可知，一次函数解析式为y=-x+4.5，
反比例函数解析式为y=
，
组成方程组得：
，
整理得出：x2-4.5x+4=0，
∴x1+x2=4.5，x1x2=4，
∵矩形B的两边长和为4.5，周长为9，面积为4，
∴这个图象所研究的矩形A的面积为8；周长为18，
故答案为：8，9；
②由题意得出：
，
解得：
，
，
则满足条件的矩形B的两边长为
和
…（12分）．
故答案为：
，
．
| 3 |
| 2 |
（2）设所求矩形的一边是x，则另一边为（
| 3 |
| 2 |
由题意得方程：x（
| 3 |
| 2 |
化简得：2x2-3x+2=0
∵b2-4ac=9-16＜0，
∴原方程无解．
∴满足要求的矩形B不存在．…（8分）
（3）（每空1分）
①由图可知，一次函数解析式为y=-x+4.5，
反比例函数解析式为y=
| 4 |
| x |
组成方程组得：
|
整理得出：x2-4.5x+4=0，
∴x1+x2=4.5，x1x2=4，
∵矩形B的两边长和为4.5，周长为9，面积为4，
∴这个图象所研究的矩形A的面积为8；周长为18，
故答案为：8，9；
②由题意得出：
|
解得：
|
|
则满足条件的矩形B的两边长为
9+
| ||
| 4 |
9-
| ||
| 4 |
故答案为：
9+
| ||
| 4 |
9-
| ||
| 4 |
点评：此题主要考查了根与系数的关系以及二元二次方程解法、利用函数图象得函数解析式等知识，根据图象得出函数解析式是解题关键．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
（2012•西城区一模）已知：如图，A点坐标为