题目内容
如图,直线y=
x+2分别交x、y轴于点A、C,P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,S△ABP=9.求:
(1)求点A、C的坐标;
(2)求反比例函数解析式;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
| 1 |
| 2 |
(1)求点A、C的坐标;

(2)求反比例函数解析式;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
(1)设A(a,0),C(0,c)由题意得
解得:
∴A(-4,0),C(0,2)
(2)根据已知条件可得A点坐标为(-4,0),
C点坐标为(0,2),
即AO=4,OC=2,
又∵S△ABP=9,
∴AB•BP=18,
又∵PB⊥x轴?OC∥PB,
∴△AOC∽△ABP,
∴
=
即
=
,
∴2BP=AB,
∴2BP2=18,
∴BP2=9,
∴BP=3,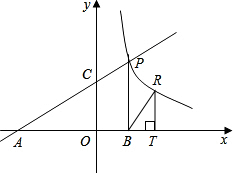
∴AB=6,
∴P点坐标为(2,3);
设反比例函数的解析式为y=
,
由题意得y=
,解得k=6
∴反比例函数的解析式为y=
;
(3)设R点的坐标为(x,y)
∵P点坐标为(2,3),
∴反比例函数解析式为y=
,
当△BTR∽△AOC时,
∴
=
,
即
=
,
则有
,
解得
,
当△BRT∽△COA时
∴
=
,
即
=
解得x1=3,x2=-1(不符合题意应舍去)
∴R的坐标为(
+1,
)或(3,2).
|
解得:
|
∴A(-4,0),C(0,2)
(2)根据已知条件可得A点坐标为(-4,0),
C点坐标为(0,2),
即AO=4,OC=2,
又∵S△ABP=9,
∴AB•BP=18,
又∵PB⊥x轴?OC∥PB,
∴△AOC∽△ABP,
∴
| AO |
| AB |
| OC |
| BP |
| 4 |
| AB |
| 2 |
| BP |
∴2BP=AB,
∴2BP2=18,
∴BP2=9,
∴BP=3,

∴AB=6,
∴P点坐标为(2,3);
设反比例函数的解析式为y=
| k |
| x |
由题意得y=
| k |
| 2 |
∴反比例函数的解析式为y=
| 6 |
| x |
(3)设R点的坐标为(x,y)
∵P点坐标为(2,3),
∴反比例函数解析式为y=
| 6 |
| x |
当△BTR∽△AOC时,
∴
| AO |
| OC |
| BT |
| RT |
即
| 4 |
| 2 |
| x-2 |
| y |
则有
|
解得
|
当△BRT∽△COA时
∴
| AO |
| OC |
| RT |
| BT |
即
| 4 |
| 2 |
| y |
| x-2 |
解得x1=3,x2=-1(不符合题意应舍去)
∴R的坐标为(
| 13 |
| ||
| 2 |

练习册系列答案
相关题目
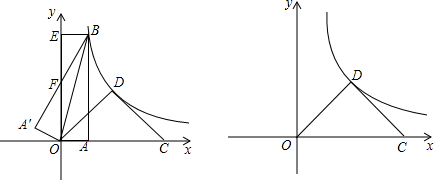


 A点左侧)是双曲线y=
A点左侧)是双曲线y=