Question

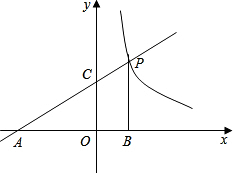
如图，点D在反比例函数y=

k

x

（k＞0）上，点C在x轴的正半轴上且坐标为（4，O），△ODC是以CO为斜边的等腰直角三角形．

（1）求点D的坐标；
（2）求反比例函数的解析式；
（3）点B为横坐标为1的反比例函数图象上的一点，BA、BE分别垂直x轴和y轴，垂足分别为点A和点E，连结OB，将四边形OABE沿OB折叠，使A点落在点A′处，A′B与y轴交于点F．求直线BA′的解析式．

Answer 1

（1）过D作DG⊥x轴，交x轴于点G，
∵△ODC为等腰直角三角形，
∴G为OC的中点，即DG为斜边上的中线，
∴DG=OG=

1

2

OC=2，
∴D（2，2），

（2）代入反比例解析式得：2=

k

2

，即k=4，
则反比例解析式为y=

4

x

；

（3）∵点B是y=

4

x

上一点，B的横坐标为1，
∴y=

4

1

=4，
∴B（1，4），
由折叠可知：△BOA′≌△BOA，
∵OA=1，AB=4，
∴BE=A′O=1，OE=BA′=4，
又∵∠OAB=90°，∠A′FO=∠BFE，
∴∠BA′O=∠OEB=90°，
∴△OA′F≌△BFE（AAS），
∴A′F=EF，
∵OE=EF+OF=4，
∴A′F+OF=4，
在Rt△A′OF中，由勾股定理得OA′²+A′F²=OF²，
设OF=x，则A′F=4-x，
∴1²+（4-x）²=x²，
∴x=

17

8

，
∴OF=

17

8

，即F（0，

17

8

），
设直线BA′解析式为y=kx+b，
将B（1，4）与F（0，

17

8

）坐标代入，
得：

k+b=4 b= 17 8

，
解得：

k= 15 8 b= 17 8

，
则线BA′解析式为y=

15

8

x+

17

8

．