题目内容
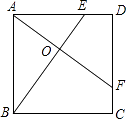
【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
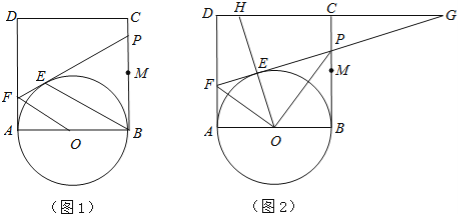
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC与H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.
【答案】(1)首先证明Rt△FAO≌Rt△FEO进而得出∠AOF=∠ABE,即可得出答案。
(2)(1<x<2)。
(3)存在这样的P点。理由见解析。
【解析】
分析:(1)首先证明Rt△FAO≌Rt△FEO进而得出∠AOF=∠ABE,即可得出答案。
(2)过F作FQ⊥BC于Q,利用勾股定理求出y与x之间的函数关系,根据M是BC中点以及BC=2,即可得出BP的取值范围。
(3)首先得出当∠EFO=∠EHG=2∠EOF时,即∠EOF=30°时,Rt△EFO∽Rt△EHG,求出y=AF=OAtan30°=![]() ,即可得出答案。
,即可得出答案。
解:(1)证明:连接OE,
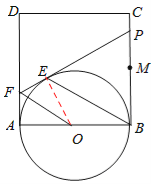
∵FE、FA是⊙O的两条切线,∴∠FAO=∠FEO=90°。
在Rt△OAF和Rt△OEF中,∵![]() ,
,
∴Rt△FAO≌Rt△FEO(HL)。
∴∠AOF=∠EOF=![]() ∠AOE。∴∠AOF=∠ABE。
∠AOE。∴∠AOF=∠ABE。
∴OF∥BE。
(2)过F作FQ⊥BC于Q,
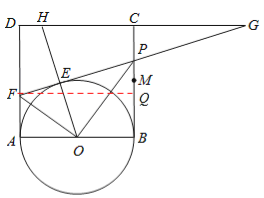
∴PQ=BP﹣BQ=x﹣y,
PF=EF+EP=FA+BP=x+y。
∵在Rt△PFQ中,FQ2+QP2=PF2,
∴22+(x﹣y)2=(x+y)2
化简得:![]() (1<x<2)。
(1<x<2)。
(3)存在这样的P点。理由如下:
∵∠EOF=∠AOF,
∴∠EHG=∠EOA=2∠EOF。
当∠EFO=∠EHG=2∠EOF时,即∠EOF=30°时,Rt△EFO∽Rt△EHG,
此时Rt△AFO中,y=AF=OAtan30°=![]() ,
,
∴![]() 。
。
∴当![]() y=
y=![]() ,时,△EFO∽△EHG。
,时,△EFO∽△EHG。

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案