题目内容
【题目】如图,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 在第二象限,过
在第二象限,过![]() 、
、![]() 两点分别作
两点分别作![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )

A.2B.![]() C.
C.![]() D.1
D.1
【答案】D
【解析】
图中直线y=x+b与x轴负半轴,y轴正半轴分别交于A,B两点,可以根据两点的坐标得出OA=OB,由此可证明△AOD≌△OBE,证出OC=AD,BE=OD,在Rt△OBE中,运用勾股定理可求出BE的长,再根据线段的差可求出DE的长.
直线y=x+b(b>0)与x轴的交点坐标A为(-b,0)与y轴的交点坐标B为(0,-b),
所以,OA=OB,
又∵AD⊥OC,BE⊥OC,
∴∠ADO=∠BEO=90°,
∵∠DOA+∠DAO=90°,∠DOA+∠DOB=90°,
∴∠DAO=∠DOB,
在△DAO和△BOE中,
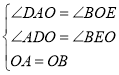
∴△DAO≌EOB,
∴OD=BE.AD=OE,
∵AD=4,
∴OE=4,
∵BE+BO=8,
∴B0=8-BE,
在Rt△OBE中,![]() ,
,
∴![]()
解得,BE=3,
∴OD=3,
∴ED=OE-OD=4-3=1.

练习册系列答案
相关题目




