题目内容
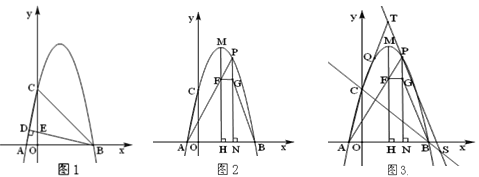
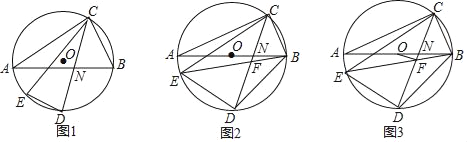
【题目】如图,△ABC内接于⊙O,弦CD平分∠ACB,点E为弧AD上一点,连接CE、DE,CD与AB交于点N.
(1)如图1,求证:∠AND=∠CED;
(2)如图2,AB为⊙O直径,连接BE、BD,BE与CD交于点F,若2∠BDC=90°﹣∠DBE,求证:CD=CE;
(3)如图3,在(2)的条件下,连接OF,若BE=BD+4,BC=![]() ,求线段OF的长.
,求线段OF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)OF=![]() .
.
【解析】
(1)连接BE,则∠CAB=∠CEB,∠BCD=∠DEB,由CD是∠ACB的平分线得∠ACD=∠BCD,从而,∠CAB+∠ACD=∠CEB+∠DEB;由∠CAB+∠ACD=∠AND可得结论;
(2)根据2∠BDC=90°-∠DBE得∠BDC+∠DBE=90°-∠BDC,由∠BDC=∠BAC得∠BDC+∠DBE=∠CFB,结合AB是直径可得∠CFB=∠CBN,从而可证明∠CDE=∠CED,故可得结论;
(3)过C作CM⊥BE,CK⊥DB易证△CEM≌△CDK,△CMB≌△CKB从而求出CM=6,作FH⊥BC于点H,FH交CM于点G,易证△CGH≌△FHB,得CG=BF,设FM=x,利用tan∠GFM=tan∠MCB=![]() =
=![]() 求得 FM=3,CF=3
求得 FM=3,CF=3![]() . 作EQ⊥DF交DF于点Q,通过△CBF∽△EDF设FQ=3k,EQ==6k,则DQ=2k,EF=3
. 作EQ⊥DF交DF于点Q,通过△CBF∽△EDF设FQ=3k,EQ==6k,则DQ=2k,EF=3![]() k,DE=2
k,DE=2![]() k得BE=5+3
k得BE=5+3![]() k,BD=BE-4=3
k,BD=BE-4=3![]() k+1,作DP⊥BE交于点P,运用勾股定理求出k的值,连接OD,在Rt△ODF中,OF2=OD2 -DF2=50-45=5,故OF=
k+1,作DP⊥BE交于点P,运用勾股定理求出k的值,连接OD,在Rt△ODF中,OF2=OD2 -DF2=50-45=5,故OF=![]() .
.
(1)证明:连接BE.
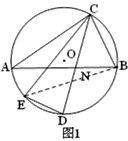
∠CED=∠CEB+∠DEB
∠AND=∠CAB+∠ACD
∵CD是∠ACB的平分线
∴∠ACD=∠BCD=∠DEB
∵∠CAB=∠CEB,
∴∠CAB+∠ACD=∠CEB+∠DEB
∠CED=∠AND;
(2)∵2∠BDC=90-∠DBE
∴∠BDC+∠DBE=90°-∠BDC
∵∠BDC=∠BAC
∴∠BDC+∠DBE=∠CFB
∴90°-∠DBE=90°-∠CAB
∵AB是直径,∴∠ACB=90
∴∠CFB=∠CBN,
∠CNB=∠CBE=∠CDE
∠CNB=∠AND=∠CED
∴∠CDE=∠CED,
∴CE=CD;
(3)过C作CM⊥BE,CK⊥DB
∴∠CME=∠CKD=90°,∠CEM=∠CDK,CE=CD
∴△CEM≌△CDK,∴EM=DK,CM=CK
∴△CMB≌△CKB,∴BM=BK
∴BE-BD=2BM=4,BM=2,∴CM=6.;
作FH⊥BC于点H,FH交CM于点G
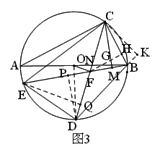
∵∠FCB=45°∴△CGH≌△FHB,∴CG=BF
设FM=x,∴CG=BF=x+2,GM=6-(x+2)=4-x
tan∠GFM=tan∠MCB=![]() =
=![]()
∴x=3,FM=3,CF=3![]() .
.
∵△CBF∽△EDF(可以用正切值相等)
作EQ⊥DF交DF于点Q
设FQ=3k,EQ==6k,则DQ=2k,EF=3![]() k,DE=2
k,DE=2![]() k
k
∴BE=5+3![]() k,BD=BE-4=3
k,BD=BE-4=3![]() k+1
k+1
作DP⊥BE交于点P,∵∠PED=∠BCD=45°,
∴PD=PE=![]() DE=2
DE=2![]() k,PB=BE-PE=5+
k,PB=BE-PE=5+![]() k;
k;
在Rt△PDB中,PB2+PD2=DB2,(5+![]() k)2+(2
k)2+(2![]() k)2=(3
k)2=(3![]() k+1)2
k+1)2
∴k=![]() , DF=5k=3
, DF=5k=3![]() =CF, BD=3
=CF, BD=3![]() k+1=10,;
k+1=10,;
∴OF⊥CD
连接OD,∴∠AOD=∠BOD=90°,∴OD=![]() BD=5
BD=5![]()
在Rt△ODF中,OF2=OD2 -DF2=50-45=5,∴OF=![]()

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
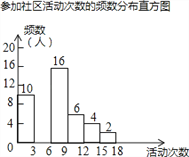
参加社区活动次数的频数、频率分布表
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | m | b |
15<x≤18 | 2 | n |
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?