题目内容
【题目】如图,菱形纸片ABCD,∠A=60°,P为AB中点,折叠菱形纸片ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC等于( )
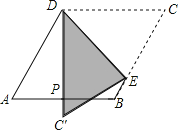
A. 60°B. 65°C. 75°D. 80°
【答案】C
【解析】
连接BD,由菱形的性质及∠A=60°,得到三角形ABD为等边三角形,P为AB的中点,利用三线合一得到DP为角平分线,得到∠ADP=30°,∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°,利用三角形的内角和定理即可求出所求角的度数.
连接BD,
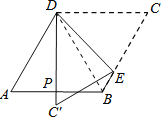
∵四边形ABCD为菱形,∠A=60°,
∴△ABD为等边三角形,∠ADC=120°,∠C=60°,
∵P为AB的中点,
∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,
∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°,
在△DEC中,∠DEC=180°-(∠CDE+∠C)=75°.
故选:C.

练习册系列答案
相关题目
【题目】为方便市民出行,甲、乙两家公司推出专车服务,运价收费如下:设行驶路程![]() 时,用含
时,用含![]() 的代数式表示乙公司的运价.
的代数式表示乙公司的运价.
行驶路程 | 收费标准 | |
甲 | 乙 | |
不超过 | 起步价6元 | 起步价7元 |
超过 | 每公里2.1元 | 每公里1.6元 |
超出 | 每公里2.2元 | |
(1)当![]() 时,则费用表示为 元;当
时,则费用表示为 元;当![]() 时,则费用表示为 元.
时,则费用表示为 元.
(2)当行驶路程![]() 时,对于乘客来说,哪个专车更合算,为什么?
时,对于乘客来说,哪个专车更合算,为什么?
(3)当行驶路程![]() 时,对于乘客来说,哪个专车更合算,为什么?
时,对于乘客来说,哪个专车更合算,为什么?