题目内容
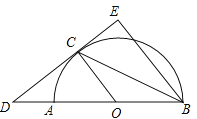
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,BE⊥CE,垂足是E,BE交AC于点D,F是BE上一点,AF⊥AE,且C是线段AF的垂直平分线上的点,AF=2![]() ,则DF=______.
,则DF=______.

【答案】3
【解析】解:连接CF,作AG⊥FE于G,过C作CH⊥AF于H.∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°.∵BE⊥EC,∴∠EBC+∠BCE=90°,∴∠EBC+∠ACE=45°.∵∠ABE+∠CBE=45°,∴∠ABF=∠ACE.∵∠BAC=∠FAE=90°,∴∠BAF=∠CAE.在△ABF和△ACE中,∵∠BAF=∠CAE,AB=AC,∠ABF=∠ACE,∴△ABF≌△ACE,∴BF=CE,AF=AE,∴△AFE是等腰直角三角形.∵AG⊥FE,∴FG=GE,AG=FG.∵AF=![]() ,∴AG=FG=GE=2.设CH与FE交于M点.∵CH⊥AF,C是线段AF的垂直平分线上的点,∴AH=FH=
,∴AG=FG=GE=2.设CH与FE交于M点.∵CH⊥AF,C是线段AF的垂直平分线上的点,∴AH=FH=![]() .∵∠AFE=45°,FM=
.∵∠AFE=45°,FM=![]() FH=2.∵FG=2,∴M与G重合,即CH过点G.∵CH⊥FA,EA⊥FA,∴CH∥EA.∵AG⊥FE,CE⊥BE,∴AG∥EC,∴四边形AGCE是平行四边形,∴GD=DE=1,∴FD=FG+DG=2+1=3.故答案为:3.
FH=2.∵FG=2,∴M与G重合,即CH过点G.∵CH⊥FA,EA⊥FA,∴CH∥EA.∵AG⊥FE,CE⊥BE,∴AG∥EC,∴四边形AGCE是平行四边形,∴GD=DE=1,∴FD=FG+DG=2+1=3.故答案为:3.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目