Question

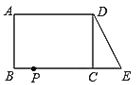
【题目】如图，在△ABC中，AD是高，E、F分别是AB、AC的中点．

（1）AB=6，AC=4，求四边形AEDF的周长；

（2）EF与AD有怎样的位置关系？证明你的结论．

Answer 1

【答案】（1）10；（2）EF垂直平分AD.

【解析】

（1）根据线段中点的性质、直角三角形的性质计算；

（2）根据线段垂直平分线的判定定理得到E、F在线段AD的垂直平分线上，得到答案．

解：（1）∵E、F分别是AB、AC的中点，

∴AE=AB=3，AF=AC=2，

∵AD是高，E、F分别是AB、AC的中点，

∴DE=AB=3，DF=AC=2，

∴四边形AEDF的周长=AE+ED+DF+FA=10；

（2）EF垂直平分AD．

证明：∵AD是△ABC的高，

∴∠ADB=∠ADC=90°，

∵E是AB的中点，

∴DE=AE， 同理：DF=AF，

∴E、F在线段AD的垂直平分线上，

∴EF垂直平分AD.