题目内容
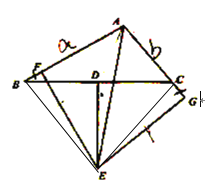
【题目】已知,如图,△ACB中,∠CAB的平分线与过BC边垂直平分线DE交于E点,EF⊥AB,垂足是F,EG⊥AC,垂足是G.

(1)求证:BF=CG;
(2)若AB=a,AC=b(a>b),求BF长(用a、b表示BF长).
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接BE,EC,根据角平分线、垂直平分线的性质得到Rt△BEF≌Rt△CEG,从而完成证明.
(2) 先证明Rt△AEF≌Rt△AEG,然后得到AF=AG,结合BF=CG,寻找和AB,AC的关系,从而完成解答.
解:(1)连接BE,EC,
∵AE平分∠BAC, EF⊥AB, EG⊥AC,
∴EF=EG
又∵BC边垂直平分线DE
∴BE=CE
在Rt△BEF和Rt△ECG中
EF=EG,BE=CE
∴Rt△BEF≌Rt△CEG
∴BF=CG
(2)在Rt△AEF和Rt△AEG中
EF=EG,AE=AE
∴Rt△AEF≌Rt△AEG
∴AF=AG
又∵BE=CG
∴AB=AF+BF=a,AG=AC+CG=b+CG=b+BF
∴AF=a-BF AG=b+BF
∴a-BF=b+BF
∴![]()

练习册系列答案
相关题目





