题目内容
【题目】如图，已知点A在反比例函数
上，作Rt△ABC，点D为斜边AC的中点，连DB并延长交y轴于点E，若△BCE的面积为8。
（1）求证：△EOB∽△ABC；
（2）求反比例函数的解析式。
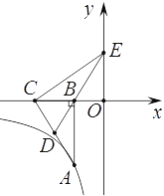
【答案】（1）证明见解析；（2）16.
【解析】根据反比例函数系数k的几何意义，证明△ABC∽△EOB，根据相似比求出BABO的值，从而求出△AOB的面积．
解：（1）∵在Rt△ABC中，点D为斜边AC的中点，
∴BD=DC，
∴∠DBC=∠DCB=∠EBO，
又∠EOB=∠ABC=90°，
∴△EOB∽△ABC
（2）∵△EOB∽△ABC
∴
=
，
∵△BCE的面积为8，
∴
=8，∵
=
，
∴BCOE=16，∴ABOB=BCOE
∴k=ABBO=BCOE=16．
∴反比例函数的解析式为： 
．
“点睛”本题考查了反比例函数系数k的几何意义，解决本题的关键是证明△EOB∽△ABC，得到ABOB=BCOE，最后求出反比例函数的解析式．
练习册系列答案
名校通行证有效作业系列答案
相关题目
