题目内容
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2 , 两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为m. 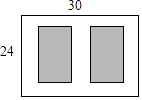
【答案】2
【解析】解:设人行通道的宽度为x米,将两块矩形绿地合在一起长为(30﹣3x)m,宽为(24﹣2x)m, 由已知得:(30﹣3x)(24﹣2x)=480,
整理得:x2﹣22x+40=0,
解得:x1=2,x2=20,
当x=20时,30﹣3x=﹣30,24﹣2x=﹣16,不符合题意舍去,
即x=2.
答:人行通道的宽度为2米.
故答案为2.
设人行通道的宽度为x米,将两块矩形绿地合在一起长为(30﹣3x)m,宽为(24﹣2x)m,根据矩形绿地的面积为480m2 , 即可列出关于x的一元二次方程,解方程即可得出x的值,经检验后得出x=20不符合题意,此题得解.

练习册系列答案
相关题目