题目内容
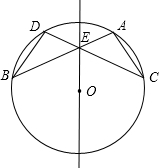如图，在⊙O中，弦AB与DC相交于点E，AB=CD．（1）求证：△AEC≌△DEB；
（2）点B与点C关于直线OE对称吗？试说明理由．
分析：（1）要证△AEC≌△DEB，由于AB=CD，根据等弦所对的弧相等得
=
，根据等量减等量还是等量，得
=
，由等弧对等弦得BD=CA，由圆周角定理得，∠ACE=∠DBE，∠AEC=∠DEB，即可根据AAS判定；
（2）由△AEC≌△DEB得，BE=CE，得到点E在直线BC的中垂线上，连接BO，CO，BO和CO是半径，则BO和CO相等，即点O在线段BC的中垂线上，亦即直线EO是线段BC的中垂线，所以点B与点C关于直线OE对称．
 |
| AB |
|
| CD |
|
| BD |
|
| CA |
（2）由△AEC≌△DEB得，BE=CE，得到点E在直线BC的中垂线上，连接BO，CO，BO和CO是半径，则BO和CO相等，即点O在线段BC的中垂线上，亦即直线EO是线段BC的中垂线，所以点B与点C关于直线OE对称．
解答：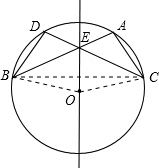
（1）证明：∵AB=CD，
∴
=
．
∴
-
=
-
．
∴
=
．
∴BD=CA．
在△AEC与△DEB中，∠ACE=∠DBE，∠AEC=∠DEB，
∴△AEC≌△DEB（AAS）．
（2）解：点B与点C关于直线OE对称．
理由如下：如图，连接OB、OC、BC．
由（1）得BE=CE．
∴点E在线段BC的中垂线上，
∵BO=CO，
∴点O在线段BC的中垂线上，
∴直线EO是线段BC的中垂线，
∴点B与点C关于直线OE对称．
（1）证明：∵AB=CD，∴
|
| AB |
|
| CD |
∴
|
| AB |
|
| AD |
|
| CD |
|
| AD |
∴
|
| BD |
|
| CA |
∴BD=CA．
在△AEC与△DEB中，∠ACE=∠DBE，∠AEC=∠DEB，
∴△AEC≌△DEB（AAS）．
（2）解：点B与点C关于直线OE对称．
理由如下：如图，连接OB、OC、BC．
由（1）得BE=CE．
∴点E在线段BC的中垂线上，
∵BO=CO，
∴点O在线段BC的中垂线上，
∴直线EO是线段BC的中垂线，
∴点B与点C关于直线OE对称．
点评：本题利用了圆周角定理、等弦所对的弧相等，等弧对等弦、全等三角形的判定和性质求解．
练习册系列答案
相关题目
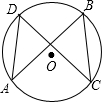已知：如图，在⊙O中，弦AD=BC．求证：AB=CD．
4、如图，在⊙O中，弦BC∥半径OA，AC与OB相交于M，∠C=20°，则∠AMB的度数为（ ）
标系．
如图，在⊙O中，弦AB=BC=CD，且∠ABC=140°，则∠AED=（ ）
如图，在⊙O中，弦AB与CD相交于点P，连接AC、DB．