Question

【题目】如图，AB是⊙O的直径，C是半圆O上的一点，AC平分∠DAB，AD⊥CD，垂足为D，AD交⊙O于E，连接CE．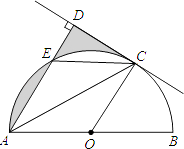
（1）判断CD与⊙O的位置关系，并证明你的结论；
（2）若E是 的中点，⊙O的半径为1，求图中阴影部分的面积．

Answer 1

【答案】
（1）解：CD与圆O相切．理由如下：

∵AC为∠DAB的平分线，

∴∠DAC=∠BAC，

∵OA=OC，

∴∠OAC=∠OCA，

∴∠DAC=∠OCA，

∴OC∥AD，

∵AD⊥CD，

∴OC⊥CD，

则CD与圆O相切

（2）解：连接EB，交OC于F，

∵E为 的中点，

∴ ，

∴AE=EC，

∴∠EAC=∠ECA，

又∵∠EAC=∠OAC，

∴∠ECA=∠OAC，

∴CE∥OA，

又∵OC∥AD，

∴四边形AOCE是平行四边形，

∴CE=OA，AE=OC，

又∵OA=OC=1，

∴四边形AOCE是菱形，

∵AB为直径，得到∠AEB=90°，

∴EB∥CD，

∵CD与⊙O相切，C为切点，

∴OC⊥CD，

∴OC∥AD，

∵点O为AB的中点，

∴OF为△ABE的中位线，

∴OF= AE= ，即CF=DE= ，

在Rt△OBF中，根据勾股定理得：EF=FB=DC= ，

则S阴影=S△DEC= × × = ．

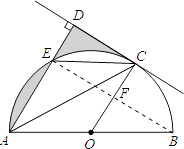
【解析】（1）CD与圆O相切，理由为：由AC为角平分线得到一对角相等，再由OA=OC，利用等边对等角得到一对角相等，等量代换得到一对内错角相等，利用内错角相等两直线平行得到OC与AD平行，根据AD垂直于CD，得到OC垂直于CD，即可得证；（2）根据E为弧AC的中点，得到弧AE=弧EC，利用等弧对等弦得到AE=EC，可得出弓形AE与弓形EC面积相等，阴影部分面积拼接为直角三角形DEC的面积，求出即可．