题目内容
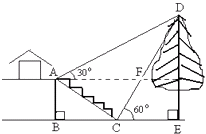
【题目】如图，在两建筑物之间有一旗杆，高15米，从A点经过旗杆顶点恰好看到矮建筑物的墙角C点，且俯角α为60°，又从A点测得D点的俯角β为30°，若旗杆底点G为BC的中点，则矮建筑物的高CD为（ ）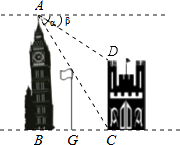
A.20米
B.10 
米
C.15 米
D.5 
米
【答案】A
【解析】解：∵点G是BC中点，EG∥AB，
∴EG是△ABC的中位线，
∴AB=2EG=30米，
在Rt△ABC中，∠CAB=30°，
则BC=ABtan∠BAC=30× 
=10 
米．
如图，过点D作DF⊥AF于点F．
在Rt△AFD中，AF=BC=10 米，
则FD=AFtanβ=10 × =10米，
综上可得：CD=AB﹣FD=30﹣10=20米．
故选：A．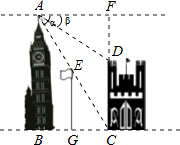
【考点精析】掌握关于仰角俯角问题是解答本题的根本，需要知道仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．
练习册系列答案
相关题目
