Question

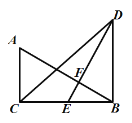
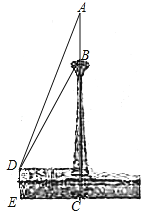
【题目】如图所示，天津电视塔顶部有一桅杆部分AB，数学兴趣小组的同学在距地面高为4.2m的平台D处观测电视塔桅杆顶部A的仰角为67.3°，观测桅杆底部B的仰角为58°．已知点A，B，C在同一条直线上，EC=172m．求测得的桅杆部分AB的高度和电视塔AC的高度．（结果保留小数点后一位）．

参考数据：tan67.3°≈2.39，tan60°≈1.73．

Answer 1

【答案】桅杆部分AB的高度为135.9m，电视塔AC的高度为415.3m．

【解析】分析：

如下图，过点D作DF⊥AC于点F，由已知易得四边形DECF是矩形，由此可得DF=EC=172m，DE=CF=4.2m，然后在Rt△ADF和Rt△BDF中结合已知条件求得AF和BF的长，即可由AB=AF-BF和AC=AF+CF求得AB和AC的长了.

详解：

如图，作DF⊥AC于点F，

∵DF∥EC，DE∥CF，DE⊥EC，

∴四边形DECF是平行四边形，∠DEC=90°，

∴四边形DECF是矩形，

∴DF=EC=172m，DE=CF=4.2m，

∵∠ADF=67.3°，∠BDF=58°，

∴在Rt△ADF中，AF=DFtan67.3°≈411.1m，

在Rt△BDF中，BF=DFtan58°≈275.2m，

∴AB=AF﹣BF=411.1﹣275.2=135.9m，

AC=AF+CF=411.1+4.2=415.3m．

答：桅杆部分AB的高度为135.9m，天塔AC的高度为415.3m．