题目内容
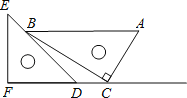
【题目】如图,正方形ABCD的边长为6,点E为BC的中点,点F在AB边上,![]() ,H在BC延长线上,且CH=AF,连接DF,DE,DH。
,H在BC延长线上,且CH=AF,连接DF,DE,DH。
(1)求证DF=DH;
(2)求![]() 的度数并写出计算过程.
的度数并写出计算过程.
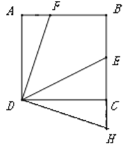
【答案】(1)详见解析;(2)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)根据正方形的性质和全等三角形的判定和性质证明即可.
(2)利用勾股定理得出Rt△DFG和Rt△EFG中,有FG2=DF2-DG2=EF2-EG2,求得DG=DF,进而解答即可.
(1)证明 ∵ 正方形ABCD的边长为6,
∴ AB=BC=CD=AD =6,![]() .
.
∴ ![]() ,
,![]() .
.
在△ADF和△CDH中,

∴ △ADF≌△CDH.(SAS)
∴ DF=DH ①
(2)连接EF
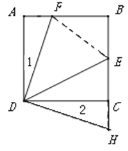
∵△ADF≌△CDH
∴![]() .
.
∴ ![]() .
.
∵ 点E为BC的中点,
∴ BE=CE=3.
∵ 点F在AB边上,![]() ,
,
∴ CH= AF=2,BF=4.
∴ ![]() .
.
在Rt△BEF中,![]() ,
,
![]() .
.
∴![]() .②
.②
又∵DE= DE,③
由①②③得△DEF≌△DEH.(SSS)
∴ ![]() .
.

练习册系列答案
相关题目
【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查,随机抽取了100个足球,检测每个足球的质量是否符合标准,超过或不足部分分别用正、负数来表示,记录如表:
与标准质量的差值(单位:克) | ﹣4 | ﹣2 | 0 | 1 | 3 | 6 |
个数 | 10 | 13 | 30 | 25 | 15 | 7 |
(1)平均每个足球的质量比标准质量多还是少?用你学过的方法合理解释;
(2)若每个足球标准质量为420克,则抽样检测的足球的总质量是多少克?