题目内容
如图,⊙C经过坐标原点O,分别交x轴正半轴、y轴正半轴于点B、A,点B的坐标为(4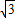 ,0),点M在⊙C上,并且∠BMO=120度.
,0),点M在⊙C上,并且∠BMO=120度.(1)求直线AB的解析式;
(2)若点P是⊙C上的点,过点P作⊙C的切线PN,若∠NPB=30°,求点P的坐标;
(3)若点D是⊙C上任意一点,以B为圆心,BD为半径作⊙B,并且BD的长为正整数.
①问这样的圆有几个?它们与⊙C有怎样的位置关系?
②在这些圆中,是否存在与⊙C所交的弧(指⊙B上的一条弧)为90°的弧,若存在,请给出证明;若不存在,请说明理由.

【答案】分析:(1)连接AB.根据圆内接四边形的性质发现60°的直角三角形,从而求得点A的坐标,根据待定系数法即可求得直线的解析式;
(2)首先根据切线的性质和角的度数能够正确分析出点P的位置,从而求得点P的坐标;
(3)①根据两圆的位置关系与数量之间的联系进行分析;
②根据圆心角的度数等于它所对的弧的度数,只需分析等腰直角三角形的边的长是否为整数.
解答: 解:(1)连接AB,
解:(1)连接AB,
∵四边形ABMO是圆内接四边形
∴∠BAO=180°-∠BMO=60°
∵OB=4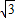
∴OA=4,即A点坐标为(O,4)
设直线AB的解析式是y=kx+b
把(0,4)和(4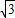 ,0),代入,得:
,0),代入,得:
4 k+4=0,k=-
k+4=0,k=-
∴直线AB解析式为- +4;
+4;
(2)点P有两种情况:
第一种情况:作CH⊥OB,垂足为H,交弧OMB于P1,P1H=2,
点P1坐标为(2 ,-2),
,-2),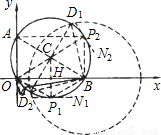
第二种情况:作直径OP2,过点P2作0C的切线P2N2,连接P2B,
点P2的坐标为(4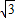 ,4),
,4),
∴点P的坐标为(2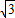 ,-2)或(4
,-2)或(4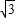 ,4);
,4);
(3)①这样的圆有8个,它们与⊙C的位置关系是相交,内切;
②不存在;
过点C作0C直径D1D2,使DlD2⊥AB,
以点B为圆心,BD为半径作圆,
则0B上的劣弧D1D2的度数为90°,
连接BD1、BD2,则△BD1D2是等腰直角三角形,
BD1=4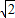 ,
,
不是正整数,∴不存在.
点评:此题要综合运用圆内接四边形的性质和特殊直角三角形的性质;
考查了两圆的位置关系以及弧的度数等于它所对的圆心角的度数.
(2)首先根据切线的性质和角的度数能够正确分析出点P的位置,从而求得点P的坐标;
(3)①根据两圆的位置关系与数量之间的联系进行分析;
②根据圆心角的度数等于它所对的弧的度数,只需分析等腰直角三角形的边的长是否为整数.
解答:
 解:(1)连接AB,
解:(1)连接AB,∵四边形ABMO是圆内接四边形
∴∠BAO=180°-∠BMO=60°
∵OB=4
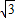
∴OA=4,即A点坐标为(O,4)
设直线AB的解析式是y=kx+b
把(0,4)和(4
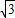 ,0),代入,得:
,0),代入,得:4
 k+4=0,k=-
k+4=0,k=-
∴直线AB解析式为-
 +4;
+4;(2)点P有两种情况:
第一种情况:作CH⊥OB,垂足为H,交弧OMB于P1,P1H=2,
点P1坐标为(2
 ,-2),
,-2),
第二种情况:作直径OP2,过点P2作0C的切线P2N2,连接P2B,
点P2的坐标为(4
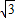 ,4),
,4),∴点P的坐标为(2
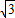 ,-2)或(4
,-2)或(4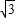 ,4);
,4);(3)①这样的圆有8个,它们与⊙C的位置关系是相交,内切;
②不存在;
过点C作0C直径D1D2,使DlD2⊥AB,
以点B为圆心,BD为半径作圆,
则0B上的劣弧D1D2的度数为90°,
连接BD1、BD2,则△BD1D2是等腰直角三角形,
BD1=4
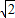 ,
,不是正整数,∴不存在.
点评:此题要综合运用圆内接四边形的性质和特殊直角三角形的性质;
考查了两圆的位置关系以及弧的度数等于它所对的圆心角的度数.

练习册系列答案
相关题目
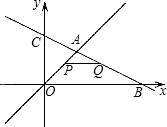 条件是
条件是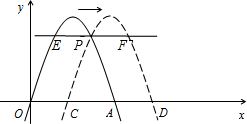 右平移m(m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P
右平移m(m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),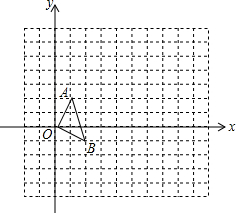 【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
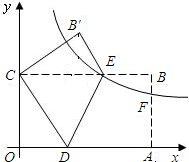 如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、BC边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.
如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、BC边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.