题目内容
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于海里.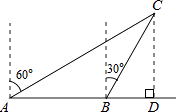
【答案】10 ![]()
【解析】解:根据题意可知∠CAD=30°,∠CBD=60°,
∵∠CBD=∠CAD+∠ACB,
∴∠CAD=30°=∠ACB,
∴AB=BC=20海里,
在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC= ![]() ,
,
∴sin60°= ![]() ,
,
∴CD=20×sin60°=20× ![]() =10
=10 ![]() 海里,
海里,
故答案为:10 ![]() .
.
根据方向角的定义及余角的性质求出∠CAD=30°,∠CBD=60°,再由三角形外角的性质得到∠CAD=30°=∠ACB,根据等角对等边得出AB=BC=20,然后解Rt△BCD,求出CD即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目