题目内容
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.点D是直线BC上方抛物线上一动点.
(1)求抛物线的解析式;
(2)如图1,连接BD、CD,设点D的横坐标为m,△BCD的面积为s.试求出s与m的函数关系式,并求出s的最大值;
(3)如图2,设AB的中点为E,作DF⊥BC,垂足为F,连接CD、CE,是否存在点D,使得以C、D,F三点为顶点的三角形与△CEO相似?若存在,请直接写出点D的坐标;若不存在,请说明理由.

【答案】(1)y=﹣x2+2x+3;(2)s与m的函数关系式为s=﹣![]() m2+
m2+![]() m,s的最大值为
m,s的最大值为![]() ;(3)点D的坐标为(
;(3)点D的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由抛物线与x轴的交点可设交点式来求解析式;
(2)过点D作DM∥y轴,交BC于点M,因为点D的横坐标为![]() ,所以
,所以![]() ,可得s与m的函数关系式为
,可得s与m的函数关系式为![]() ,即可利用配方求出最大值;
,即可利用配方求出最大值;
(3)根据题意可知以C、D,F三点为顶点的三角形与△CEO相似,∠CFD=∠COE=90°可分为两种情况:△CFD∽△COE或△CFD∽△EOC,再利用相等角的三角函数值相等的关系式得到等量关系,解方程即可求得m的值
解:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0)
∴y=﹣(x+1)(x﹣3)=﹣x2+2x+3
∴抛物线解析式为y=﹣x2+2x+3
(2)过点D作DM∥y轴,交BC于点M如图1:
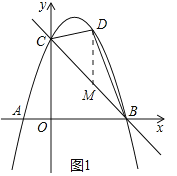
∵当x=0时,y=﹣x2+2x+3=3
∴C(0,3)
∴直线BC解析式为![]()
∵点D的横坐标为![]()
∴![]()
∴![]()
∴![]()
∴s与m的函数关系式为![]() ,s的最大值为
,s的最大值为![]() .
.
(3)存在点D,使得以C、D,F三点为顶点的三角形与△CEO相似
如图2,连接BD
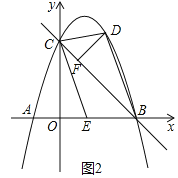
∵点E为AB中点,A(﹣1,0),B(3,0),C(0,3)
∴E(1,0),OE=1,OC=3,![]()
∴![]()
∴![]() ,
,![]()
∵![]() ,DF⊥BC
,DF⊥BC
∴![]()
∴![]()
∵以C、D,F三点为顶点的三角形与△CEO相似,∠CFD=∠COE=90°
∴△CFD∽△COE或△CFD∽△EOC
① 若△CFD∽△COE,则∠FCD=∠OCE
∴![]()
∴![]()
∴![]()
解得:![]()
∴![]()
∴![]()
② 若△CFD∽△EOC,则∠FDC=∠OCE
∴![]()
∴![]()
∴![]()
解得:![]()
∴![]()
∴![]()
∴点D的坐标为![]() 或
或![]() .
.

 习题精选系列答案
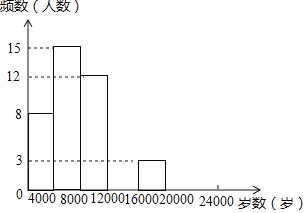
习题精选系列答案【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
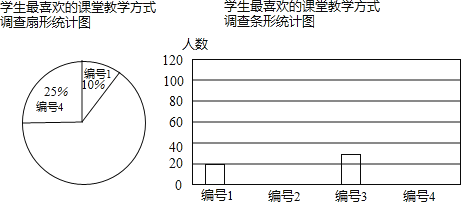
【题目】某中学为促进课堂教学,提高教学质量,对九年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.
(1)请把三个图表中的空缺部分都补充完整;
(2)你最喜欢以上哪一种教学方式或另外的教学方式,请提出你的建议,并简要说明理由(字数在20字以内).
编号 | 教学方式 | 最喜欢的频数 | 频率 |
1 | 教师讲,学生听 | 20 | 0.10 |
2 | 教师提出问题,学生探索思考 | 0.5 | |
3 | 学生自行阅读教材,独立思考 | 30 | |
4 | 分组讨论,解决问题 | 0.25 |