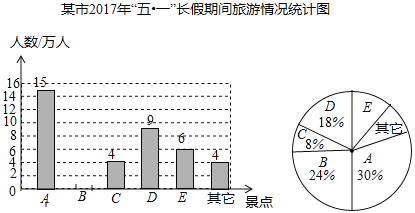
��Ŀ����
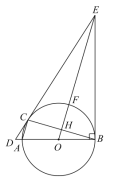
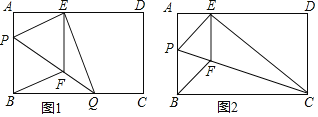
����Ŀ����ͼ1���ھ���ֽƬABCD�У�AB��12cm��AD��20cm���۵�ֽƬʹB�����ڱ�AD�ϵ�E�����ۺ�ΪPQ������E��EF��AB��PQ��F������BF��
��1����֤���ı���BFEPΪ���Σ�
��2������E��AD�����ƶ�ʱ���ۺ۵Ķ˵�P��QҲ��֮�ƶ���
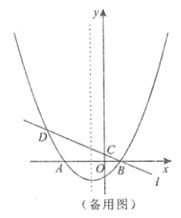
�ٵ���Q���C�غ�ʱ����ͼ2����������BFEP�ı߳���
������P��Q�ֱ��ڱ�BA��BC���ƶ��������E�ڱ�AD���ƶ��������룮
���𰸡���1��֤������������2��������BFEP�ı߳�Ϊ![]() cm���ڵ�E�ڱ�AD���ƶ���������Ϊ8cm��
cm���ڵ�E�ڱ�AD���ƶ���������Ϊ8cm��
��������
��1�����۵������ʵó�PB=PE��BF=EF����BPF=��EPF����ƽ���ߵ����ʵó���BPF=��EFP��֤����EPF=��EFP���ó�EP=EF�����BP=BF=EF=EP�����ɵó����ۣ�
��2�����ɾ��ε����ʵó�BC=AD=20cm��CD=AB=12cm����A=��D=90�����ɶԳƵ����ʵó�CE=BC=20cm����Rt��CDE�У��ɹ��ɶ������DE=16cm���ó�AE=AD-DE=4cm����Rt��APE�У��ɹ��ɶ����ó����̣��ⷽ�̵ó�EP=![]() cm���ɣ�
cm���ɣ�
�ڵ���Q���C�غ�ʱ����E���A������ɢ�֪����ʱAE=4cm������P���A�غ�ʱ����E���A��Զ����ʱ�ı���ABQEΪ�����Σ�AE=AB=3cm�����ɵó��𰸣�
��1��֤�������۵�ֽƬʹB�����ڱ�AD�ϵ�E�����ۺ�ΪPQ��
���B���E����PQ�Գƣ�
��PB��PE��BF��EF����BPF����EPF��
�֡�EF��AB��
���BPF����EFP��
���EPF����EFP��
��EP��EF��
��BP��BF��EF��EP��
���ı���BFEPΪ���Σ�
��2���١��ı���ABCD�Ǿ��Σ�
��BC��AD��20cm��CD��AB��12cm����A����D��90����
�ߵ�B���E����PQ�Գƣ�
��CE��BC��20cm��
��Rt��CDE��DE��![]() ��16cm��
��16cm��
��AE��AD��DE��20cm��16cm��4cm��
��Rt��APE��AE��4��AP��12��PB��12��PE��
��EP2��42+��12��EP��2��
��ã�EP��![]() cm��
cm��
������BFEP�ı߳�Ϊ![]() cm��
cm��
�ڵ���Q���C�غ�ʱ����ͼ2��

��E���A������ɢ�֪����ʱAE��4cm��
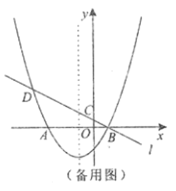
����P���A�غ�ʱ����ͼ3��ʾ��
��E���A��Զ����ʱ�ı���ABQEΪ�����Σ�AE��AB��12cm��
���E�ڱ�AD���ƶ���������Ϊ8cm