题目内容
如图,Rt△ABC中,∠BAC=90°,AB=AC=2,点D为BC边上的动点(D不与B、C重合),∠AD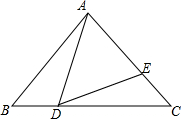 E=45°,DE交AC于点E.
E=45°,DE交AC于点E.(1)∠BAD与∠CDE的大小关系为
(2)设BD=x,AE=y,求y关于x的函数关系式,并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长;
(4)是否存在x,使△DCE的面积是△ABD面积的2倍?若存在,求出x的值,若不存在,请说明理由.
分析:(1)由AB=AC易知△ABC是等腰直角三角形,即∠B=∠C=45°,已知∠ADE=45°,由三角形内角和定理以及平角的定义可得∠BAD、∠CDE都等于180°-45°-∠ADB,由此可证得两角相等.
(2)由(1)的等角,联立∠B=∠C=45°,可证得△DCE∽△ABD,根据相似三角形所得比例线段,即可表示出CE的长,进而由AE=AC-CE求得y、x的函数关系式.
(3)由于D与B、C不重合,显然∠ADE=∠AED=45°不符合题意,即AD≠AE,所以此题分两种情况讨论:
①AD=DE,此时(2)的相似三角形全等,由此可求得CD、BD的长,进而可得CE、AE的值;
②AE=DE,此时∠DAE=45°,即AD平分∠BAC,由于△BAC是等腰直角三角形,根据等腰三角形三线合一的性质可知AD垂直平分BC,同理可证得DE垂直平分AC,即AE为AC长的一半,由此得解.
(4)若△DCE的面积是△ABD面积的2倍,根据相似三角形的面积比等于相似比的平方可知:CE=
BD,然后表示出AE的长,代入(2)的函数关系式中,即可求得x的值,若x=0,则说明D、B重合,显然不存在符合条件的x,若x的值符合(2)的自变量取值范围,那么x的值即为所求.
(2)由(1)的等角,联立∠B=∠C=45°,可证得△DCE∽△ABD,根据相似三角形所得比例线段,即可表示出CE的长,进而由AE=AC-CE求得y、x的函数关系式.
(3)由于D与B、C不重合,显然∠ADE=∠AED=45°不符合题意,即AD≠AE,所以此题分两种情况讨论:
①AD=DE,此时(2)的相似三角形全等,由此可求得CD、BD的长,进而可得CE、AE的值;
②AE=DE,此时∠DAE=45°,即AD平分∠BAC,由于△BAC是等腰直角三角形,根据等腰三角形三线合一的性质可知AD垂直平分BC,同理可证得DE垂直平分AC,即AE为AC长的一半,由此得解.
(4)若△DCE的面积是△ABD面积的2倍,根据相似三角形的面积比等于相似比的平方可知:CE=
| 2 |
解答:(本小题满分14分)
解:(1)相等;(1分)
证明如下:∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°.如图1,
∵∠1+∠B+∠ADB=180°,
∴∠1+∠ADB=180°-∠B=135°.
又∵∠2+∠ADE+∠ADB=180°,
∴∠2+∠ADB=180°-∠ADE(2分)
=180°-45°=135°,
即∠1+∠ADB=∠2+∠ADB,
∴∠1=∠2.(3分)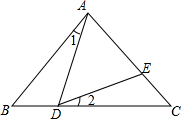
(2)由(1)知∠1=∠2,又∵∠B=∠C=45°,
∴△DCE∽△ABD.(4分)
若BD=x,则CD=BC-BD=2
-x,
由△DCE∽△ABD得
=
,即
=
,
CE=
(2
-x)x,
=-
x2+
x,(5分)
y=AE=AC-CE=2-(-
x2+
x)
∴y=
x2-
x+2,(6分)
其中0<x<2
.(7分)
(3)解:∵点D不能与B点重合,∴AD=AE不能成立(8分)
(或:∵∠ADE=45°,若AD=AE,
则∠AED=ADE=45°,从而∠DAE=90°,
即B与D重合,这与已知条件矛盾).
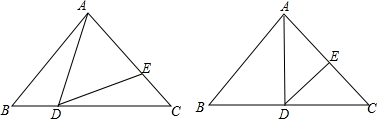
①当AE、DE为腰,即AE=DE时(如图2),
∠EAD=∠EDA=45°,此时,AD平分∠BAC,
∴D为BC边的中点(“三线合一”性质),
且E也为AC边的中点,∴AE=1;(9分)
②当AD、DE为腰,即AD=DE时(如图3),
由(1)△ABD∽△DCE知,此时AD与DE为对应边,
∴△ABD≌△DCE,DC=AB=2,
BD=BC-CD=2
-2,AE=AC-EC
=2-BD=2-(2
-2)=4-2
;(10分)
综上所述,当△ADE是等腰三角形时,
AE的长为1或4-2
;(11分)
(4)不存在.(12分)
原因如下:∵△DCE∽△ABD,若△DCE的面积是△ABD面积的2倍,则
=2,
从而
=
,CE=
BD,-
x2+
x=
x,
解得x=0,即BD=0,就是说D点与B点重合,(13分)
这与已知条件矛盾,
∴不存在x,使△DCE的面积是△ABD面积的2倍.(14分)
解:(1)相等;(1分)
证明如下:∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°.如图1,
∵∠1+∠B+∠ADB=180°,
∴∠1+∠ADB=180°-∠B=135°.
又∵∠2+∠ADE+∠ADB=180°,
∴∠2+∠ADB=180°-∠ADE(2分)
=180°-45°=135°,
即∠1+∠ADB=∠2+∠ADB,
∴∠1=∠2.(3分)

(2)由(1)知∠1=∠2,又∵∠B=∠C=45°,
∴△DCE∽△ABD.(4分)
若BD=x,则CD=BC-BD=2
| 2 |
由△DCE∽△ABD得
| CE |
| BD |
| CD |
| AB |
| CE |
| x |
2
| ||
| 2 |
CE=
| 1 |
| 2 |
| 2 |
=-
| 1 |
| 2 |
| 2 |
y=AE=AC-CE=2-(-
| 1 |
| 2 |
| 2 |
∴y=
| 1 |
| 2 |
| 2 |
其中0<x<2
| 2 |
(3)解:∵点D不能与B点重合,∴AD=AE不能成立(8分)
(或:∵∠ADE=45°,若AD=AE,
则∠AED=ADE=45°,从而∠DAE=90°,
即B与D重合,这与已知条件矛盾).
①当AE、DE为腰,即AE=DE时(如图2),
∠EAD=∠EDA=45°,此时,AD平分∠BAC,
∴D为BC边的中点(“三线合一”性质),
且E也为AC边的中点,∴AE=1;(9分)
②当AD、DE为腰,即AD=DE时(如图3),
由(1)△ABD∽△DCE知,此时AD与DE为对应边,
∴△ABD≌△DCE,DC=AB=2,
BD=BC-CD=2
| 2 |
=2-BD=2-(2
| 2 |
| 2 |
综上所述,当△ADE是等腰三角形时,
AE的长为1或4-2
| 2 |

(4)不存在.(12分)
原因如下:∵△DCE∽△ABD,若△DCE的面积是△ABD面积的2倍,则
| S△CDE |
| S△ABD |
从而
| CE |
| BD |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
解得x=0,即BD=0,就是说D点与B点重合,(13分)
这与已知条件矛盾,
∴不存在x,使△DCE的面积是△ABD面积的2倍.(14分)
点评:此题主要考查了等腰直角三角形的性质以及相似三角形的判定和性质,同时还涉及到分类讨论的数学思想,难度较大.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.