题目内容
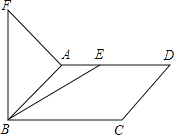
【题目】如图,在平行四边形ABCD中,AB=2,∠ABC=45°,点E为射线AD上一动点,连接BE,将BE绕点B逆时针旋转60°得到BF,连接AF,则AF的最小值是_____.
【答案】![]()
【解析】
如图,以AB为边向下作等边△ABK,连接EK,在EK上取一点T,使得AT=TK.再证明△ABF≌△KBE,可得AF=EK;然后根据垂线段最短可知,当KE⊥AD时,KE的值最小,最后解直角三角形求出EK即可.
解:如图,以AB为边向下作等边△ABK,连接EK,在EK上取一点T,使得AT=TK.

∵BE=BF,BK=BA,∠EBF=∠ABK=60°,
∴∠ABF=∠KBE,
∴△ABF≌△KBE(SAS),
∴AF=EK,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠ABC=45°,
∴∠BAD=180°﹣∠ABC=135°,
∵∠BAK=60°,
∴∠EAK=75°,
∵∠AEK=90°,
∴∠AKE=15°,
∵TA=TK,
∴∠TAK=∠AKT=15°,
∴∠ATE=∠TAK+∠AKT=30°,
设AE=a,则AT=TK=2a,ET=![]() a,
a,
在Rt△AEK中,
∵AK2=AE2+EK2,
∴a2+(2a+![]() a)2=2
a)2=2![]() ,
,
∴a=![]() ,
,
∴EK=2a+![]() a=
a=![]() ,
,
∴AF的最小值为![]() .
.
故答案为![]() .
.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】某学校为了了解九年级学生上学期间平均每天的睡眠情况,现从全校![]() 名九年级学生中随机抽取了部分学生,调查了这些同学上学期间平均每天的睡眠时间
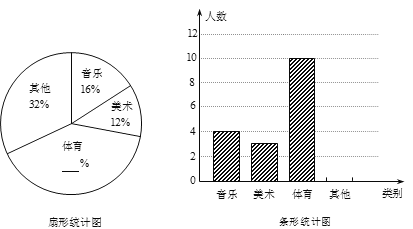
名九年级学生中随机抽取了部分学生,调查了这些同学上学期间平均每天的睡眠时间![]() (单位:小时),并根据调查结果列出统计表,绘制成扇形统计图,如图所示.请你根据图表提供的信息解答下列问题:
(单位:小时),并根据调查结果列出统计表,绘制成扇形统计图,如图所示.请你根据图表提供的信息解答下列问题:
平均每天睡眠时间分组统计表
组别序号 | 睡眠时间 | 人数(频数) |
|
|
|
|
|
|
|
|
|
|
|
|
平均每天睡眠时间扇形统计表
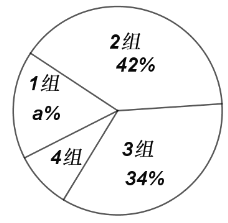
(1)![]() _______,
_______,![]() _______,
_______,![]() _______(
_______(![]() 为百分号前的数字);
为百分号前的数字);
(2)随机抽取的这部分学生平均每天睡眠时间的中位数落在_______组(填组别序号);
(3)估计全校![]() 名九年级学生中平均每天睡眠时间不低于
名九年级学生中平均每天睡眠时间不低于![]() 小时的学生有_______名;
小时的学生有_______名;
(4)若所抽查的睡眠时间![]() (小时)的
(小时)的![]() 名学生,其中
名学生,其中![]() 名男生和
名男生和![]() 名女生,现从这
名女生,现从这![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加个别访谈,请用列表或画树状图的方法求选取的
名学生参加个别访谈,请用列表或画树状图的方法求选取的![]() 名学生恰为
名学生恰为![]() 男
男![]() 女的概率.
女的概率.