题目内容
下列结论正确的是（ ）
①方程
=-2没有实数根；
②解方程（
）2-2（
）=0时，若设y=
，则原方程变形为y2-2y-3=0；
③存在这样的两个实数a、b，使得
+
=
；
④当a≠0时，关于x的方程ax=b总有实数根．
①方程
| x-1 |
②解方程（
| x |
| x-1 |
| x |
| x-1 |
| x |
| x-1 |
③存在这样的两个实数a、b，使得
| a |
| b |
| a-b |
④当a≠0时，关于x的方程ax=b总有实数根．
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
分析：根据二次根式的意义、换元法、一元一次方程的解法分别分析各个选项．
解答：解：算术平方根应是非负数，故方程
=-2没有实数根，①正确；
用换元法替换后，为y2-2y=0，②错误；
当b=0，a≥0时，式子成立，③正确；
当a≠0时，关于x的方程ax=b总有实数根，为x=
，④正确．
故选C．
| x-1 |
用换元法替换后，为y2-2y=0，②错误；
当b=0，a≥0时，式子成立，③正确；
当a≠0时，关于x的方程ax=b总有实数根，为x=
| b |
| a |
故选C．
点评：一个数的算术平方根一定是非负数，用换元法可使方程简化，当a≠0时，关于x的方程ax=b总有实数根，为x=
．
| b |
| a |
练习册系列答案
相关题目
下列结论正确的是（ ）
A、
| ||
B、当x=-3时，分式
| ||
| C、（-a+b）（-a-b）=a2-b2 | ||
| D、a2+a3=a5 |
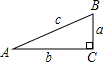如图，在Rt△ABC中，∠C=90°，BC=a，CA=b，AB=C，则下列结论正确的是（ ）A、sinB=
| ||
B、cosB=
| ||
C、tanB=
| ||
D、cotB=
|
如果-b是a的立方根（ab≠0），那么下列结论正确的是（ ）
| A、-b也是-a的立方根 | B、b是a的立方根 | C、b是-a的立方根 | D、以上结论均不正确 |
